
 ,
,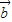 ,
,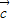 满足|
满足|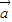 |=1,|
|=1,|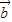 |=2,
|=2,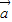 ,
, 的夹角等于
的夹角等于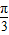 ,且(
,且(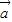 -
- )•(
)•(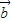 -
-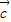 )=0,则|
)=0,则|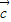 |的取值范围是 .
|的取值范围是 . 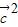 =|
=|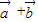 |•|
|•|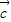 |cosα-1,α为
|cosα-1,α为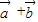 与
与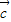 的夹角,再由
的夹角,再由 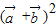 =
=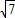 求出|
求出| |=
|=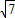 ,解得cosα=
,解得cosα=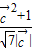 .由于 0≤α≤π,-1≤cosα≤1,可得
.由于 0≤α≤π,-1≤cosα≤1,可得 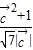 ≤1,即
≤1,即 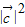 -
-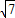 |
| |+1≤0,由此求得|
|+1≤0,由此求得|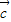 |的取值范围是.
|的取值范围是.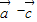 )•(
)•(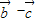 )=0 可得
)=0 可得 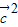 =(
=(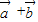 )•
)•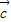 -
-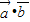 =|
=|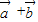 |•|
|•|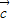 |cosα-1×2cos
|cosα-1×2cos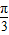 =|
=|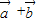 |•|
|•|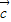 |cosα-1,α为
|cosα-1,α为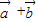 与
与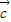 的夹角.
的夹角.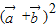 =
=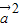 +
+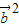 +2
+2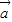 •
•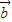 =1+4+2×1×2cos
=1+4+2×1×2cos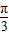 =7 可得|
=7 可得|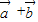 |=
|=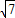 ,
,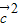 =
=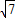 |
| |cosα-1,解得cosα=
|cosα-1,解得cosα=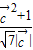 .
.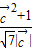 ≤1,即
≤1,即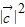 -
-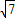 |
|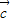 |+1≤0.
|+1≤0.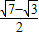 ≤|
≤|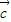 |≤
|≤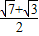 ,
,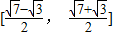 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012-2013学年辽宁省沈阳市高三高考领航考试(一)理科数学试卷(解析版) 题型:选择题
已知平面向量 ,且满足
,且满足 。若
。若 ,则 ( )
,则 ( )
A. 有最大值-2 B.z有最小值-2 C.z有最大值-3 D.z有最小值-3
有最大值-2 B.z有最小值-2 C.z有最大值-3 D.z有最小值-3
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省成都市高三三诊模拟考试理科数学 题型:选择题
已知平面向量 ,且满足
,且满足 。若
。若
 ,则 ( )
,则 ( )
A. 有最大值-2 B.z有最小值-2 C.z有最大值-3 D.z有最小值-3
有最大值-2 B.z有最小值-2 C.z有最大值-3 D.z有最小值-3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com