练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    选修4—5：不等式选讲

    已知函数

    （Ⅰ）当时，求不等式 的解集；

    （Ⅱ）证明： [来源:学科网Z

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届江苏南通中学高三上期中数学（理）试卷（解析版） 题型：解答题

    在平面直角坐标系xOy中，已知曲线C： （?为参数，?∈R），直线l： （t为参数，t∈R），求曲线C上的动点P到直线l的距离的最小值．

    查看答案和解析>>

    科目：高中数学 来源：2017届湖北荆荆襄宜四地七校联盟高三文上联考一数学试卷（解析版） 题型：选择题

    已知与的夹角为，其中，，则（ ）

    A． B．

    C． D．

    查看答案和解析>>

    科目：高中数学 来源：2017届湖北荆荆襄宜四地七校联盟高三理上联考一数学试卷（解析版） 题型：选择题

    已知函数，设，且，若、、成等差数列，则

    A． B．

    C． D．的符号不确定

    查看答案和解析>>

    科目：高中数学 来源：2017届湖北荆荆襄宜四地七校联盟高三理上联考一数学试卷（解析版） 题型：选择题

    下列选项中，说法正确的是

    A．命题“，”的否定为“，”

    B．命题“在中，，则”的逆否命题为真命题

    C．若非零向量、满足，则与共线

    D．设是公比为的等比数列，则“”是“为递增数列”的充分必要条件

    查看答案和解析>>

    科目：高中数学 来源：2017届广东韶关市六校高三10月联考数学（文）试卷（解析版） 题型：解答题

    如图，是底面边长为2，高为的正三棱柱，经过AB的截面与上底面相交于PQ， 设.

    （Ⅰ）证明：；

    （Ⅱ）当时，求点C到平面APQB的距离.

    查看答案和解析>>

    科目：高中数学 来源：2017届广东韶关市六校高三10月联考数学（文）试卷（解析版） 题型：选择题

    对于三次函数，给出定义：设是函数的导数，是的导数，若方程=0有实数解，则称点（，）为函数的“拐点”．经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．设函数，则=（ ）

    A．100 B．50 C． D．0

    查看答案和解析>>

    科目：高中数学 来源：2016-2017学年湖北孝感市七校联盟高二理上期中数学试卷（解析版） 题型：解答题

    甲、乙两人练习罚球，每人练习6组，每组罚球20个，命中个数的茎叶图如下：

    （1）求甲命中个数的中位数和乙命中个数的众数；

    （2）通过计算，比较甲乙两人的罚球水平．

    查看答案和解析>>

    科目：高中数学 来源：2017届山东省青州市高三10月段测数学试卷（解析版） 题型：解答题

    已知，，，（）．

    （1）求函数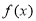的值域；

    （2）设△的内角，，的对边分别为，，，若，，，求的值．

    查看答案和解析>>

    同步练习册答案