
若 ,且
,且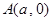 、
、 、
、 三点共线,则
三点共线,则 的最小值为 .
的最小值为 .
16
【解析】
试题分析:解:根据题意,A(a,0)、B(0,b)、C(-2,-2)三点共线,可得kAB=kBC,即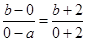 ,化简可得2a+2b+ab=0,即ab=-2a-2b,若ab>0,要么a>0且b>0,要么a<0且b<0,直线经过第三象限的C(-2,-2),由直线的性质可知,a<0,b<0,因为a<0,b<0,所以-2a-2b>0且-2a-2b≥2
,化简可得2a+2b+ab=0,即ab=-2a-2b,若ab>0,要么a>0且b>0,要么a<0且b<0,直线经过第三象限的C(-2,-2),由直线的性质可知,a<0,b<0,因为a<0,b<0,所以-2a-2b>0且-2a-2b≥2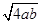 =4
=4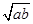 又因为ab=-2a-2b,所以ab≥4
又因为ab=-2a-2b,所以ab≥4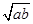 ,即ab-4
,即ab-4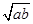 ≥0,令t=
≥0,令t=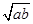 >0,可得t2-4t≥0,解可得t≥4或t≤0,又由t>0,则t≥4,即
>0,可得t2-4t≥0,解可得t≥4或t≤0,又由t>0,则t≥4,即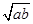 ≥4,ab≥16;则ab的最小值为16;故答案为16.
≥4,ab≥16;则ab的最小值为16;故答案为16.
考点:基本不等式
点评:本题考查基本不等式的应用,涉及三点共线的问题,有一定的难度;解题的难点在于利用基本不等式对(-2a-2b)变形,可得ab≥4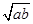 ,进而由一元二次不等式的性质来求解
,进而由一元二次不等式的性质来求解


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源:2014届安徽省宿州市高一下学期期中质量检测数学试卷(解析版) 题型:选择题
已知等差数列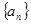 的前
的前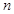 项和为
项和为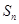 ,若
,若 ,且
,且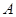 、
、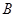 、
、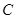 三点共线(该直线不过点
三点共线(该直线不过点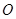 ),则
),则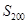 等于( )
等于( )
A.100 B.200 C.101 D.201
查看答案和解析>>
科目:高中数学 来源:2010年贵州省遵义市高三考前最后一次模拟测试数学(理)试题 题型:选择题
已知等差数列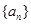 的前
的前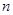 项和为
项和为 ,若
,若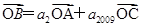 ,且
,且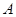 、
、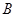 、
、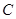 三点共线(该直线不过原点
三点共线(该直线不过原点 ),则
),则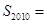 ( )
( )
A.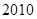 B.
B.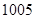 C.
C.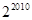 D.
D.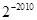
查看答案和解析>>
科目:高中数学 来源:2010年福建省宁德市阶段性考试数学卷 题型:填空题
下面有5个命题:
①分针每小时旋转 弧度;
弧度;
②若 ,且
,且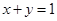 ,则
,则 三点共线;
三点共线;
③在同一坐标系中,函数 的图象和函数
的图象和函数 的图象有三个公共点;
的图象有三个公共点;
④函数 是奇函数;
是奇函数;
⑤在 中,若
中,若 ,则
,则 。
。
其中,真命题的编号是___________(写出所有真命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
下面三道题中任选两道作答:
(1)已知圆C的参数方程为![]() (
(![]() 为参数),P是圆C与y轴的交点,若以圆心C为极点,x 轴的正半轴为极轴建立极坐标系,则过点P圆C的切线的极坐标方程是 .
为参数),P是圆C与y轴的交点,若以圆心C为极点,x 轴的正半轴为极轴建立极坐标系,则过点P圆C的切线的极坐标方程是 .
(2)若![]() ,且
,且![]() 、
、![]() 、
、![]() 三点共线,则
三点共线,则![]() 的最小值为 .
的最小值为 .
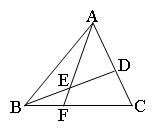
(3)如图,在△ABC中,D是AC的中点,E是BD的中点,AE交BC于F,则![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com