
使一块矩形木板ABCD的一边AB靠紧桌面α,并绕AB转动.AB的对边CD在各个位置时,是不是都和桌面α平行?为什么?
科目:高中数学 来源: 题型:
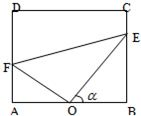 某居民小区内建有一块矩形草坪ABCD,AB=50米,BC=25
某居民小区内建有一块矩形草坪ABCD,AB=50米,BC=25| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,某学校的教学楼前有一块矩形空地ABCD,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为a米与b米(a与b均不小于2米),且要求“转角处”(图中矩形AEFG)的面积为8平方米.
如图所示,某学校的教学楼前有一块矩形空地ABCD,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为a米与b米(a与b均不小于2米),且要求“转角处”(图中矩形AEFG)的面积为8平方米.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,某学校的教学楼前有一块矩形空地ABCD,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为a米与b米均不小于2米,且要求“转角处(图中矩形AEFG)”的面积为8平方米
如图所示,某学校的教学楼前有一块矩形空地ABCD,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为a米与b米均不小于2米,且要求“转角处(图中矩形AEFG)”的面积为8平方米查看答案和解析>>
科目:高中数学 来源: 题型:
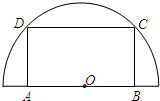 (2013•闵行区二模)如图,在半径为20cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.
(2013•闵行区二模)如图,在半径为20cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com