
(得分不计入总成绩)已知二次函数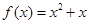 ,若不等式
,若不等式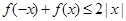 的解集为
的解集为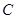 .
.
(1)求集合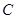 ;
;
(2)若方程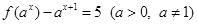 在
在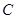 上有解,求实数
上有解,求实数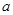 的取值范围;
的取值范围;
(3)记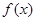 在
在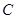 上的值域为
上的值域为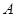 ,若
,若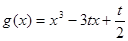 ,
,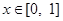 的值域为
的值域为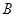 ,且
,且
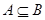 ,求实数
,求实数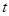 的取值范围.
的取值范围.
(1)C=[-1,1]
(2)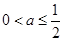 或a≥5;(3)
或a≥5;(3)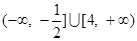
【解析】第一问中,利用绝对值不等式求解得到解集,
当x≥0时,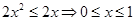
当x<0时,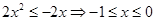
第二问中,方程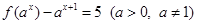 在
在 上有解,即
上有解,即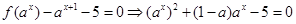 令ax=u
令ax=u
设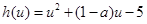 ∵
∵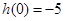
当a>1时,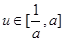 ,h(u)=0在
,h(u)=0在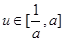 上有解
上有解
当0<a<1时,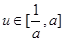 ,h(u)=0在
,h(u)=0在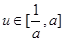 上有解,
上有解,
所以∴当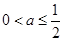 或a≥5时,方程在C上有解,且有唯一解。
或a≥5时,方程在C上有解,且有唯一解。
第三问中,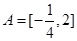 ,
,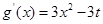
t≤0时,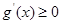 ,函数
,函数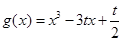 在x∈[0,1]单调递增,
在x∈[0,1]单调递增,
∴ 函数g(x)的值域
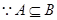 所以则有
所以则有
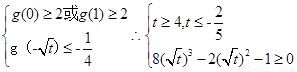
从而得到范围。
解:(1) f(x)+f(-x)=2x2
当x≥0时,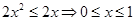
当x<0时,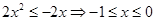
∴集合C=[-1,1] ------------2分
(2)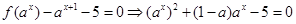 ,令ax=u
,令ax=u
设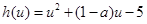 ∵
∵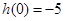
当a>1时,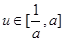 ,h(u)=0在
,h(u)=0在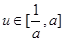 上有解,
上有解,
则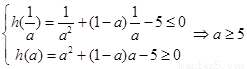 ------------4分
------------4分
当0<a<1时,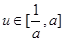 ,h(u)=0在
,h(u)=0在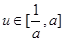 上有解,
上有解,
则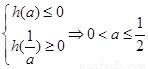 -------------6分
-------------6分
∴当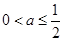 或a≥5时,方程在C上有解,且有唯一解。 -------------7分
或a≥5时,方程在C上有解,且有唯一解。 -------------7分
(3)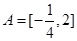 ,
,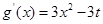
①当t≤0时,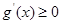 ,函数
,函数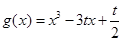 在x∈[0,1]单调递增,
在x∈[0,1]单调递增,
∴ 函数g(x)的值域 ,
,
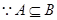 ,
,
 --------9分
--------9分
②当t≥1,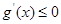 ,函数g(x)在区间[0,1]单调递减,
,函数g(x)在区间[0,1]单调递减,

又t≥1,所以t≥4 ----------11分
③当0<t<1时,令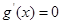 得
得 (舍去负值),
(舍去负值),
当 时,
时, ,当
,当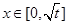 时,
时, .
.
∴函数g(x)在 单调递增;在
单调递增;在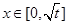 单调递减,g(x)在
单调递减,g(x)在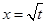 达到最小值。
达到最小值。
要使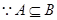 ,则
,则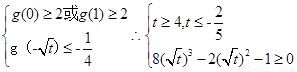

,无解。 -------------14分
综上所述:t的取值范围是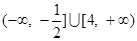 。
-------------15分
。
-------------15分


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com