
求当函数y=sin2x+acosx- a-
a-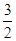 的最大值为1时a的值.
的最大值为1时a的值.
y=1-cos2x+acosx-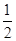 a-
a-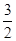
=-cos2x+acosx-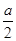 -
-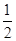
=-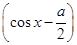 2+
2+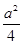 -
-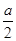 -
-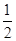 .
.
设cosx=t,∵-1≤cosx≤1,
∴-1≤t≤1.
∴y=-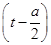 2+
2+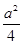 -
-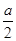 -
-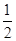 ,-1≤t≤1. ………2分
,-1≤t≤1. ………2分
(1)当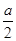 <-1,即a<-2时,t=-1,y有最大值-
<-1,即a<-2时,t=-1,y有最大值-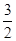 a-
a-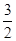 .
.
由已知条件可得-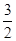 a-
a-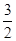 =1,∴a=-
=1,∴a=-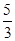 >-2(舍去).
……5分
>-2(舍去).
……5分
(2)当-1≤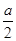 ≤1时,即-2≤a≤2时,t=
≤1时,即-2≤a≤2时,t=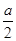 ,y有最大值
,y有最大值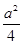 -
-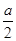 -
-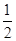 .
.
由已知条件可得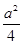 -
-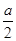 -
-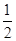 =1,解得a=1-
=1,解得a=1- 或a=1+
或a=1+ (舍去).……8分
(舍去).……8分
(3)当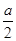 >1,即a>2时,t=1,y有最大值
>1,即a>2时,t=1,y有最大值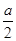 -
-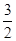 .
.
由已知条件可得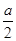 -
-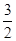 =1,∴a=5.
………11分
=1,∴a=5.
………11分
综上可得a=1- 或a=5.
或a=5.
【解析】略


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:潮阳一中2007届高三摸底考试理科数学 题型:044
知函数
y=sin2ωx+求:当
X∈[0,π]0时y的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com