


 之间的矩形的高,并完成直方图;
之间的矩形的高,并完成直方图; 之间任取两份进行分析,在抽取的结果中,求至少有一份分数在
之间任取两份进行分析,在抽取的结果中,求至少有一份分数在 之间的概率.
之间的概率.
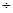 样本容量,得参赛总人数,再由[80,90的频率除以组距10,求出[80,90)之间的矩形的高;(2)由已知中的茎叶图,可以求出分数在[80,90]和[90,100]之间的频数,然后列举出在[80,100]之间任取两份的基本事件个数及在[90,100]之间的基本事件个数,代入古典概型概率公式,可得答案.
样本容量,得参赛总人数,再由[80,90的频率除以组距10,求出[80,90)之间的矩形的高;(2)由已知中的茎叶图,可以求出分数在[80,90]和[90,100]之间的频数,然后列举出在[80,100]之间任取两份的基本事件个数及在[90,100]之间的基本事件个数,代入古典概型概率公式,可得答案.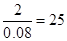 ,又分数在[80,90)之间的人数为25-2-7-10-2=4,∴分数在[80,90)之间的频率为
,又分数在[80,90)之间的人数为25-2-7-10-2=4,∴分数在[80,90)之间的频率为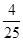 =0.16,得频率分布直方图中[80,90)间矩形的高为
=0.16,得频率分布直方图中[80,90)间矩形的高为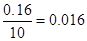 ,完成直方图,如下图,
,完成直方图,如下图,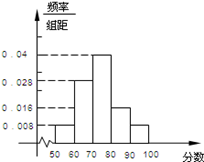 ;
;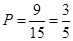 .
.

科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

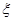 ,试求
,试求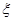 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com