
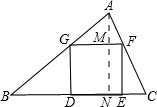
 解:如图,作AN⊥BC于N交GF与M,
解:如图,作AN⊥BC于N交GF与M,| AM |
| AN |
| GF |
| BC |
| h-x |
| h |
| x |
| a |
| ah |
| a+h |
| ah |
| a+h |
| 8 |
| a+h |
| 8 | ||
2
|
| 2 |
| 2 |


科目:高中数学 来源:2013届山东省济南世纪英华实验学校高二下期中理科数学试卷(解析版) 题型:解答题
如图所示,现有一边长为6的正方形铁板,如果从铁板的四个角各截出去一个相同的小正方形,做成一个长方体形的无盖容器为使其容积最大,截下的小正方形边长应为多少?

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2012年黑龙江省哈尔滨三中高考数学四模试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2013年山东省高考数学预测试卷(13)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com