分析:(1)由题意取AA1的中点P利用题中的N是A1D的中点,得到线面垂直,在得到线线垂直进而线线平行即可得正中点;
(2)由题意及(1)知∠PNM即为MN与平面ADD1A1所成的角,然后在三角形中解出即可;
(3)因为N是A1D的中点,M是BB1的中点,得到三角形相似,在△AMN中,作AG⊥MN交MN于G,得到二面角的平面角,在三角形中解出.
解答: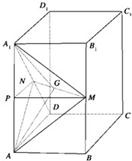
解:(1)证明:取AA
1的中点P,连接PM,PN.
∵N是A
1D的中点,∴AA
1⊥PN,又∵AA
1⊥MN,MN∩PN=N,
∴AA
1⊥面PMN.
∵PM?面PMN,∴AA
1⊥PM,∴PM∥AB,
∴点M是BB
1的中点.
(2)由(1)知∠PNM即为MN与平面ADD
1A
1所成的角.
在Rt△PMN中,易知PM=1,PN=
,
∴tan∠PNM=
=2,∠PNM=arctan2.
故MN与平面ADD
1A
1所成的角为arctan2.
(3)∵N是A
1D的中点,M是BB
1的中点,∴A
1N=AN,A
1M=AM,
又MN为公共边,∴△A
1MN≌△AMN.
在△AMN中,作AG⊥MN交MN于G,连接A
1G,则∠A
1GA即为二面角A-MN-A
1的平面角.
在△A
1GA中,AA
1=2,A
1G=GA=
,
∴cos∠A
1GA=
=-
,∴∠A
1GA=arccos(-
),
故二面角A-MN-A
1的大小为arccos(-
).
点评:此题重点考查了利用线线垂直得到线面垂直在得到线线垂直,利用同一个平面内垂直同一条直线的两条直线平行的性质,还考查了利用二面角平面角的定义求出二面角的大小及反三角的表示角的大小的知识,此还考查了余弦定理求角的大小.

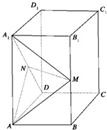 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,N是A1D的中点,M∈BB1,异面直线MN与A1A所成的角为90°.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,N是A1D的中点,M∈BB1,异面直线MN与A1A所成的角为90°. 解:(1)证明:取AA1的中点P,连接PM,PN.
解:(1)证明:取AA1的中点P,连接PM,PN.

 如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点.
如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点. 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′= (2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=
(2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1= 如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点. (2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )
(2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )