
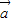 、
、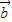 、
、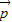 ,则下列命题中正确命题的序号:
,则下列命题中正确命题的序号: 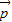 =x
=x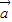 +y
+y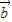 ,则
,则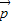 与
与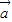 、
、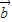 共面;
共面; 与
与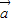 、
、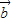 共面,则
共面,则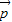 =x
=x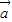 +y
+y ;
;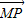 =x
=x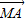 +y
+y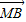 ,则P、M、A、B共面;
,则P、M、A、B共面;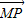 =x
=x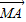 +y
+y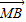
 +μ
+μ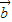 =0,则λ=μ=0
=0,则λ=μ=0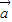 ,
,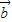 不共线,则空间任一向量p=λ
不共线,则空间任一向量p=λ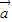 +μ
+μ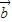 (λ,μ∈R)
(λ,μ∈R) 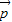 =x
=x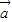 +y
+y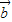 ,则由平面向量基本定理得
,则由平面向量基本定理得 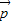 与
与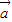 、
、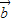 共面,故 ①正确.
共面,故 ①正确.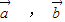 都是零向量,而
都是零向量,而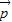 为非零向量时,此等式不成立.
为非零向量时,此等式不成立.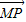 =x
=x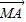 +y
+y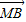 ,则
,则 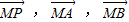 共面,故四点 P、M、A、B共面,故③正确.
共面,故四点 P、M、A、B共面,故③正确.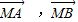 ,而
,而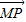 为非零向量时,此关系不成立.
为非零向量时,此关系不成立.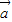 和
和 互为反向量时,
互为反向量时,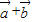 =0,此时,λ=μ=1.
=0,此时,λ=μ=1.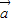 ,
,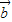 不共线,当
不共线,当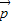 与
与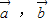 所在平面垂直时,
所在平面垂直时,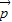 =λ
=λ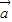 +μ
+μ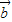 (λ,μ∈R) 不成立.
(λ,μ∈R) 不成立.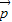 =x
=x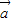 +y
+y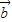 ,则由平面向量基本定理得
,则由平面向量基本定理得 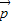 与
与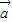 、
、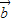 共面,故 ①正确.
共面,故 ①正确.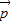 与
与 、
、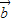 共面,则
共面,则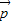 =x
=x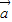 +y
+y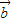 不一定成立,如
不一定成立,如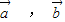 都是零向量,而
都是零向量,而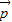 为非零向量时,此等式不成立.
为非零向量时,此等式不成立.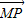 =x
=x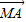 +y
+y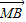 ,则
,则 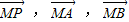 共面,故四点 P、M、A、B共面,故③正确.
共面,故四点 P、M、A、B共面,故③正确.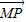 =x
=x +y
+y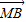 不一定成立,如
不一定成立,如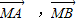 ,而
,而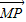 为非零向量时,此关系不成立.
为非零向量时,此关系不成立. +μ
+μ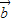 =0,则λ=μ=0不一定成立,如
=0,则λ=μ=0不一定成立,如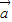 和
和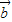 互为反向量时,
互为反向量时,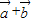 =0,此时,λ=μ=1.
=0,此时,λ=μ=1.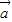 ,
,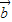 不共线,当
不共线,当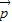 与
与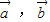 所在平面垂直时,
所在平面垂直时,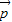 =λ
=λ +μ
+μ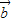 (λ,μ∈R) 不成立.
(λ,μ∈R) 不成立.

科目:高中数学 来源: 题型:
| p |
| a |
| b |
| c |
| p |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| i |
| j |
| k |
| i |
| j |
| i |
| j |
| k |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| p |
| a |
| b |
| c |
| p |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| i |
| j |
| k |
| i |
| j |
| i |
| j |
| k |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都市树德中学高二(上)期中数学试卷(理科)(解析版) 题型:填空题
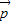 可由三个不共面的向量
可由三个不共面的向量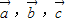 唯一确定地表示为
唯一确定地表示为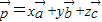 ,则称(x,y,z)为基底
,则称(x,y,z)为基底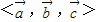 下的广义坐标.特别地,当
下的广义坐标.特别地,当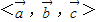 为单位正交基底时,(x,y,z)为直角坐标.设
为单位正交基底时,(x,y,z)为直角坐标.设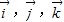 分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底
分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底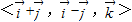 下的广义坐标为 .
下的广义坐标为 .查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都市树德中学高二(上)期中数学试卷(理科)(解析版) 题型:填空题
 可由三个不共面的向量
可由三个不共面的向量 唯一确定地表示为
唯一确定地表示为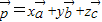 ,则称(x,y,z)为基底
,则称(x,y,z)为基底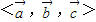 下的广义坐标.特别地,当
下的广义坐标.特别地,当 为单位正交基底时,(x,y,z)为直角坐标.设
为单位正交基底时,(x,y,z)为直角坐标.设 分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底
分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底 下的广义坐标为 .
下的广义坐标为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com