
(12分)在甲、乙等6个单位参加的一次“唱读讲传”演出活动中,每个单位的节目集中安排在 一起. 若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,……,6),求:
一起. 若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,……,6),求:
(Ⅰ)甲、乙两单位的演出序号均为偶数的概率;
(Ⅱ)甲、乙两单位的演出序号不相邻的概率.
用(a,b)表示甲和乙的位置,有如下30 种等可能的基本事件。
种等可能的基本事件。
(1,2),(1,3)(1,4),(1,5),(1,6)
(2,1),(2,3)(2,4),(2,5), (2,6)
(2,6)
(3,1),(3,2)(3,4),(3,5),(3,6)
(4,1),(4,2)(4,3),(4,5),(4,6)
(5,1),(5,2)(5,3),(5,4),(5,6)
(6,1),(6,2)(6,3),(6,4),(6,5)
(Ⅰ)设A表示“甲、乙两单位的演出序号均为偶数”
则A包含如下6种基本事件:(2,4),(2,6),(4,2),(4,6),(6,2),(6,4)
据古典概型概率公式,故所求概率为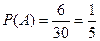
(Ⅱ)设B表示“甲、乙两单位的演出序号不相邻”
则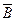 表示“甲、乙两单位的演出序号相邻”
表示“甲、乙两单位的演出序号相邻” 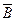 包含如
包含如 下10种基本事件:
下10种基本事件:
(1,2),(2,3),(3,4),(4,5),(5,6)
(2,1),(3,2),(4,3),(5,4),(6,5),
据古典概型概率公式,从而所求概率为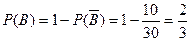
解析


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源:2012-2013学年安徽省马鞍山高三三模理科数学试卷(解析版) 题型:解答题
(本小题满分12分)甲、乙等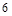 名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为
名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为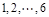 ).
).
(Ⅰ)求甲、乙两考生的面试序号至少有一个为奇数的概率;
(Ⅱ)记在甲、乙两考生之间参加面试的考生人数为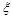 ,求随机变量
,求随机变量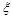 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省五校协作体高三摸底考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)甲、乙等五名环保志愿者被随机地分到 四个不同的岗位服务,每个岗位至少有一名志愿者.
四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加 岗位服务的概率;
岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)设随机变量 为这五名志愿者中参加
为这五名志愿者中参加 岗位服务的人数,求
岗位服务的人数,求 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源:2010年河北省高二第二学期期末考试数学(文)试卷 题型:解答题
(本小题满分12分)
甲、乙等五名奥运志愿者被随机地分到 四个不同的岗位服务,每个岗位至少有一名志愿者.
四个不同的岗位服务,每个岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加 岗位服务的概率;
岗位服务的概率;
(Ⅱ)求甲、乙两人不在同一个岗位服务的概率。
查看答案和解析>>
科目:高中数学 来源:2010-2011年黑龙江省高二第二学期期中考试文科数学 题型:解答题
(12分)在甲、乙等6个单位参加的一次“唱读讲传”演出活动中,每个单位的节目集中安排在一起. 若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,……,6),求:
(Ⅰ)甲、乙两单位的演出序号均为偶数的概率;
(Ⅱ)甲、乙两单位的演出序号不相邻的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com