Question

某自来水厂的蓄水池中有400吨水，每天零点开始从池中放水，向居民供水，同时以每小时60吨的速度向池中注水，t小时内向居民供水总量为120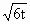(0≤t≤24)．

(1)每天几点时蓄水池中的存水量最少？

(2)若池中存水量不多于80吨时，就会出现供水紧张现象，则每天会有几小时出现这种现象？

Answer 1

答案：
解析：

解：(1)设从零点开始t小时后，蓄水池存水量为f(t)，则f(t)＝400＋60t－120(0≤t≤24)，令x＝，则x∈[0，12]，f(t)＝400＋10(x2－12x)＝10(x－6)2＋40≥40，当且仅当x＝6时，即t＝6时，上式等号成立，故6点钟时，蓄水池中的存水量最少，最少存水量为40吨． 　　(2)设f(t)≤80(0≤t≤24)，则有10(－6)2＋40≤80，解得≤t≤． 　　故每天2：40至10：40供水紧张，有8小时出现这种现象．