练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图2-4-12，P为⊙O的直径CB延长线上的一点，A为⊙O上一点，若=，AE交BC于D，且∠C=∠PAD.

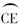
    图2-4-12

    (1)求证：PA为⊙O的切线；

    (2)若∠BEA=30°，BD=1，求AP及PB长.

    思路分析:对于（1），A已经是圆上一点，所以可以连结OA，证明PA与OA垂直；对于（2），将∠E利用圆周角定理转移到Rt△ODA和Rt△OAP中，解直角三角形即可得到线段AP及PB的长.

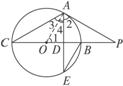
    （1）证明:连结AO，∵=，BC为直径，∴AE⊥BC，AD=DE，=.

    ∵OA=OC，∴∠C=∠3.∴∠1=2∠C.

    又∵∠C=∠PAD，∴∠1=∠2.

    ∵∠1＋∠4=90°，∴∠2＋∠4=90°.

    ∴PA⊥OA.

    ∴PA为⊙O的切线.

    （2）解:在Rt△EBD中，∵∠BEA=30°，BD=1,∴BE=2，DE=.

    在Rt△ODA和Rt△EBD中,∠4=90°-∠1=90°-2∠C=90°-2∠E=30°=∠E，∠ODA=∠BDE，AD=ED，

    ∴Rt△ODA≌Rt△EBD.

    ∴AD=DE=，OD=BD=1，OA=BE=2.

    在Rt△OAP中，∵AD⊥OP，

    ∴AD2=OD·DP，即()2=1·DP.

    ∴DP=3.∴BP=2.

    在Rt△ADP中，根据勾股定理，得AP=.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

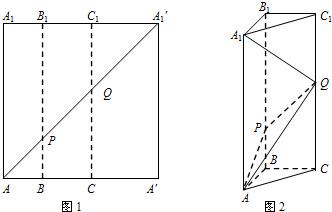    精英家教网如图1所示，在边长为12的正方形AA′A1′A1中，点B，C在线段AA′上，且AB=3，BC=4，作BB1∥AA1，分别交A1A1′、AA1′于点B1、P，作CC1∥AA1，分别交A1A1′、AA1′于点C1、Q，将该正方形沿BB1、CC1折叠，使得A′A1′与AA1重合，构成如图2所示的三棱柱ABC-A1B1C1．
    （1）在三棱柱ABC-A1B1C1中，求证：AB⊥平面BCC1B1；
    （2）求平面APQ将三棱柱ABC-A1B1C1分成上、下两部分几何体的体积之比．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    19、如图1，在边长为12的正方形AA′A′1A1中，BB1∥CC1∥AA1，且AB=3，BC=4，AA′1分别交BB1，CC1于点P、Q，将该正方形沿BB1、CC1折叠，使得A′A′1与AA1重合，构成如图2所示的三棱柱ABC-A1B1C1，请在图2中解决下列问题：
    （1）求证：AB⊥PQ；
    （2）在底边AC上有一点M，满足AM；MC=3：4，求证：BM∥平面APQ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图1所示，在边长为12的正方形ADD1A1中，点B，C在线段AD上，且AB=3，BC=4，作BB1∥AA1，分别交A1D1，AD1于点B1，P，作CC1∥AA1，分别交A1D1，AD1于点C1，Q，将该正方形沿BB1，CC1折叠，使得DD1与AA1重合，构成如图2所示的三棱柱ABC-A1B1C1．
    （Ⅰ）求证：AB⊥平面BCC1B1；
    （Ⅱ）求四棱锥A-BCQP的体积；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图2-4-12,P为⊙O的直径CB延长线上的一点,A为⊙O上一点,若=,AE交BC于D,且∠C =∠PAD.

    图2-4-12

    (1)求证:PA为⊙O的切线;

    (2)若∠BEA =30°,BD ＝1,求AP及PB的长.

    查看答案和解析>>

    同步练习册答案