
| 1 | 4 |
| |5k| | ||
|
| 5 |
| 1 |
| 4 |
| 8 |
| 3 |
| 16+4m |
| 3 |
| y2 |
| 28 |
| y2 |
| a2 |
| 7 |
| x12 |
| 28 |
| y12 |
| a2 |
| x22 |
| 28 |
| y22 |
| a2 |
| (x1-x2)(x1+x2) |
| 28 |
| (y1-y2)(y1+y2) |
| a2 |
| |5k| | ||
|
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 8 |
| 3 |
| 16+4m |
| 3 |
| x2 |
| 28 |
| y2 |
| 7 |
| y2 |
| 28 |
| y2 |
| a2 |
| 7 |
| x12 |
| 28 |
| y12 |
| a2 |
| x22 |
| 28 |
| y22 |
| a2 |
| (x1-x2)(x1+x2) |
| 28 |
| (y1-y2)(y1+y2) |
| a2 |
| y1-y2 |
| x1-x2 |
| x0 |
| 28 |
| 4y0 |
| a2 |
| x |
| 28 |
| 4y |
| a2 |
| a2 |
| 112 |
| 1 |
| 2 |
| x2 |
| 28 |
| y2 |
| 56 |
| 1 |
| 2 |
| 7 |
2
| ||
| 3 |
10
| ||
| 3 |
2
| ||
| 3 |
10
| ||
| 3 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 2 |
| 1 |
| 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013��ɽ��ʡ�����и߶���ѧ����ĩ����������ѧ ���ͣ������
(��������12��)
��֪˫����G��������ԭ��,���Ľ�������Բx2��y2��10x��20��0����.����P(��4,0)��б��Ϊ��ֱ��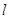 ,ʹ��
,ʹ��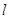 ��G����A,B����,��y�ύ�ڵ�C,���ҵ�P���߶�AB��,������|PA|��|PB|��|PC|2.
��G����A,B����,��y�ύ�ڵ�C,���ҵ�P���߶�AB��,������|PA|��|PB|��|PC|2.
(1)��˫����G�Ľ����ߵķ��̣�
(2)��˫����G�ķ��̣�
(3)��ԲS��������ԭ��,���Ķ�����G��ʵ��.���S�д�ֱ��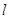 ��ƽ���ҵ��е�Ĺ켣ǡ����G�Ľ����߽���S�ڵIJ���AB,��P��x,y����y>0��Ϊ��Բ��һ��,��
��ƽ���ҵ��е�Ĺ켣ǡ����G�Ľ����߽���S�ڵIJ���AB,��P��x,y����y>0��Ϊ��Բ��һ��,��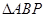 ��������ʱ��P������.
��������ʱ��P������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013�켪��ʡ�߶���ѧ���������������ѧ ���ͣ������
.��֪˫����G��������ԭ��,���Ľ�������Բx2��y2��10x��20��0����.����P(��4,0)��б��Ϊ��ֱ��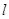 ,ʹ��
,ʹ��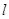 ��G����A,B����,��y�ύ�ڵ�C,���ҵ�P���߶�AB��,������|PA|��|PB|��|PC|2.
��G����A,B����,��y�ύ�ڵ�C,���ҵ�P���߶�AB��,������|PA|��|PB|��|PC|2.
(1)��˫����G�Ľ����ߵķ��̣�
(2)��˫����G�ķ��̣�
(3)��ԲS��������ԭ��,���Ķ�����G��ʵ��.���S�д�ֱ��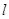 ��ƽ���ҵ��е�Ĺ켣ǡ����G�Ľ����߽���S�ڵIJ���AB,��P��x,y����y>0��Ϊ��Բ��һ��,��
��ƽ���ҵ��е�Ĺ켣ǡ����G�Ľ����߽���S�ڵIJ���AB,��P��x,y����y>0��Ϊ��Բ��һ��,��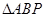 ��������ʱ��P������.
��������ʱ��P������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com