
分析 (Ⅰ)求出函数的导数,计算f′(1),f(1),求出切线方程即可;
(Ⅱ)求出函数f(x)的导数,通过讨论a的范围,判断函数的单调性结合函数的零点个数求出a的范围即可;
(Ⅲ)当a=0时,f(x)-g(x)=(x-1)ex+ex-lnx-x-1.设h(x)=xex-lnx-x-1,其定义域为(0,+∞),只需证明h(x)>0即可.
解答 解:(Ⅰ)当a=1时,函数f(x)=xex+x2,
因为f'(x)=xex+2x,所以f'(1)=e+2.又f(1)=1,
则所求的切线方程为y-1=(e+2)(x-1).
化简得:y=(e+2)x-e-1.…(3分)
(Ⅱ)因为f'(x)=x(ex+2a)
①当a=0时,函数f(x)=(x-1)ex只有一个零点;
②当a>0,函数当x∈(-∞,0)时,f'(x)<0;
函数当x∈(0,+∞)时,f'(x)>0.
所以f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增.
又f(0)=-1,f(1)=a,
因为x<0,所以x-1<0,ex<1,所以ex(x-1)>x-1,所以g(x)>ax2+x-1
取${x_0}=\frac{{-1-\sqrt{1+4a}}}{2a}$,显然x0<0且g(x0)>0
所以f(0)f(1)<0,f(x0)f(0)<0.
由零点存在性定理及函数的单调性知,函数有两个零点.
③当a<0时,由f'(x)=x(ex+2a)=0,得x=0,或x=ln(-2a).
若$a≥-\frac{1}{2}$,则ln(-2a)≤0.
故当x∈(0,+∞)时,f'(x)>0,所以函数f(x)在(0,+∞)在单调递增,
所以函数f(x)在(0,+∞)至多有一个零点.
又当x∈(-∞,0)时,f(x)<0,所以函数f(x)在(-∞,0)上没有零点.
所以函数f(x)不存在两个零点.
若$a<-\frac{1}{2}$,则ln(-2a)>0.当(ln(-2a),+∞)时,f'(x)>0,
所以函数f(x)在(ln(-2a),+∞)上单调递增,
所以函数f(x)在(ln(-2a),+∞)至多有一个零点.
当x∈(-∞,0)时,f'(x)>0;当x∈(0,ln(-2a))时,f'(x)<0;
所以函数f(x)在(-∞,0)上单增,(0,ln(-2a))上单调递减,
所以函数f(x)在(-∞,ln(-2a))上的最大值为f(0)=-1<0,
所以函数f(x)在(-∞,ln(-2a))上没有零点.
所以f(x)不存在两个零点.
综上,a的取值范围是(0,+∞).…(9分)
( III)证明:当a=0时,f(x)-g(x)=(x-1)ex+ex-lnx-x-1.
设h(x)=xex-lnx-x-1,其定义域为(0,+∞),则证明h(x)>0即可.
因为$h'(x)=(x+1){e^x}-\frac{x+1}{x}$,所以h'(0.1)<0,h'(1)>0.
又因为$h''(x)=(x+2){e^x}+\frac{1}{x^2}>0$,所以函数h'(x)在(0,+∞)上单调递增.
所以h'(x)=0有唯一的实根x0∈(0,1),且${e^{x_0}}=\frac{1}{x_0}$.
当0<x<x0时,h'(x)<0;当x>x0时,h'(x)>0.
所以函数h(x)的最小值为h(x0).
所以$h(x)≥h({x_0})={x_0}{e^{x_0}}-ln{x_0}-{x_0}-1$=1+x0-x0-1=0.
所以f(x)-g(x)≥0.…(14分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,函数零点问题,是一道综合题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:解答题
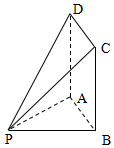 如图,四边形ABCD为矩形,PB=2,BC=3,PA⊥平面ABCD.
如图,四边形ABCD为矩形,PB=2,BC=3,PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
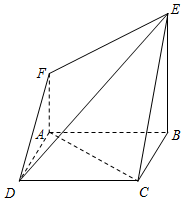 在如图所示的几何体中,四边形ABCD为正方形,四边形ABEF为直角梯形,且AF∥BE,AB⊥BE,平面ABCD∩平面ABEF=AB,AB=BE=2AF=2.
在如图所示的几何体中,四边形ABCD为正方形,四边形ABEF为直角梯形,且AF∥BE,AB⊥BE,平面ABCD∩平面ABEF=AB,AB=BE=2AF=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | B. | $\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$ | C. | $\frac{4}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | D. | $\frac{2}{3}\overrightarrow{AB}+\frac{5}{3}\overrightarrow{AC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
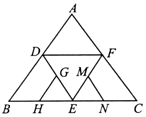 如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,有以下结论:
如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,有以下结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
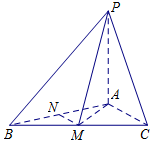 在三棱锥P-ABC中,PA⊥平面ABC,AB=AC=2,BC=2$\sqrt{3}$,M,N分别为BC,AB中点.
在三棱锥P-ABC中,PA⊥平面ABC,AB=AC=2,BC=2$\sqrt{3}$,M,N分别为BC,AB中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com