练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    点A.(1,2),B(4,5),O为坐标原点,=+t.若点P在第二象限,求实数t的取值范围.

    活动:教师引导学生利用向量的坐标运算以及向量的相等,把已知条件转化为含参数的方程(组)或不等式(组)再进行求解.教师以提问的方式来了解学生组织步骤的能力,或者让学生到黑板上去板书解题过程,并对思路清晰过程正确的同学进行表扬,同时也要对组织步骤不完全的同学给与提示和鼓励.教师要让学生明白“化归”思想的利用.不等式求变量取值范围的基本观点是,将已知条件转化为关于变量的不等式(组),那么变量的取值范围就是这个不等式(组)的解集.

    解:由已知=(4,5)-(1,2)=(3,3).∴=(1,2)+t(3,3)=(3t+1,3t+2).

    若点P在第二象限,则

    故t的取值范围是(-,-).

    点评:此题通过向量的坐标运算,将点P的坐标用t表示,由点P在第二象限可得到一个关于t的不等式组,这个不等式组的解集就是t的取值范围.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2010年高考试题分项版理科数学之专题四三角函数 题型：解答题

    （14分）在平面直角坐标系xOy中，点A(-1,-2),B(2,3),C(-2,-1)

    （1）求以线段AB、AC为邻边的平行四边形两条对角线的长

    （2）设实数t满足(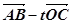)·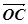=0，求t的值

     

    查看答案和解析>>

    科目：高中数学 来源：2010年高考试题分项版理科数学之专题十五推理与证明 题型：解答题

    （14分）在平面直角坐标系xOy中，点A(-1,-2),B(2,3),C(-2,-1)

    （1）求以线段AB、AC为邻边的平行四边形两条对角线的长

    （2）设实数t满足(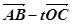)·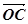=0，求t的值

     

    查看答案和解析>>

    科目：高中数学 来源：2010年高考试题分项版理科数学之专题十七选修系列 题型：解答题

    （14分）在平面直角坐标系xOy中，点A(-1,-2),B(2,3),C(-2,-1)

    （1）求以线段AB、AC为邻边的平行四边形两条对角线的长

    （2）设实数t满足(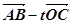)·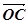=0，求t的值

     

    查看答案和解析>>

    科目：高中数学 来源：2010年高考试题分项版理科数学之专题九立体几何 题型：解答题

    （14分）在平面直角坐标系xOy中，点A(-1,-2),B(2,3),C(-2,-1)

    （1）求以线段AB、AC为邻边的平行四边形两条对角线的长

    （2）设实数t满足(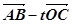)·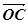=0，求t的值

     

    查看答案和解析>>

    科目：高中数学 来源：2011年内蒙古包头一中高一第一学期期末考试数学理卷 题型：解答题

    （本小题满分12分）
    在平面直角坐标系xOy中，点A(-1,-2),B(2,3),C(-2,-1)
    (1)求以线段AB、AC为邻边的平行四边形两条对角线的长;
    (2)设实数t满足(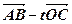)·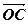=0，求t的值.

    查看答案和解析>>

    同步练习册答案