
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为 ![]() . (Ⅰ)求椭圆C的方程;
. (Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为 ![]() ,求△AOB面积的最大值.
,求△AOB面积的最大值.
【答案】解:(Ⅰ)设椭圆的半焦距为c,依题意 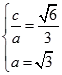 ∴b=1,∴所求椭圆方程为
∴b=1,∴所求椭圆方程为 ![]() . (Ⅱ)设A(x1 , y1),B(x2 , y2).
. (Ⅱ)设A(x1 , y1),B(x2 , y2).
①当AB⊥x轴时, ![]() .
.
②当AB与x轴不垂直时,设直线AB的方程为y=kx+m.
由已知 ![]() ,得
,得 ![]() .
.
把y=kx+m代入椭圆方程,整理得(3k2+1)x2+6kmx+3m2﹣3=0,
∴ ![]() ,
, ![]() .
.
∴|AB|2=(1+k2)(x2﹣x1)2
= 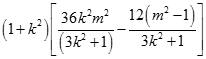
= 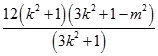
= 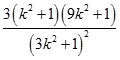
= ![]()
= 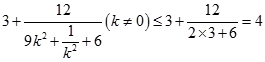 .
.
当且仅当 ![]() ,即
,即 ![]() 时等号成立.当k=0时,
时等号成立.当k=0时, ![]() ,
,
综上所述|AB|max=2.∴当|AB|最大时,△AOB面积取最大值 ![]()
【解析】(Ⅰ)设椭圆的半焦距为c,依题意求出a,b的值,从而得到所求椭圆的方程.(Ⅱ)设A(x1 , y1),B(x2 , y2).(1)当AB⊥x轴时, ![]() .(2)当AB与x轴不垂直时,设直线AB的方程为y=kx+m.由已知
.(2)当AB与x轴不垂直时,设直线AB的方程为y=kx+m.由已知 ![]() ,得
,得 ![]() .把y=kx+m代入椭圆方程,整理得(3k2+1)x2+6kmx+3m2﹣3=0,然后由根与系数的关系进行求解.
.把y=kx+m代入椭圆方程,整理得(3k2+1)x2+6kmx+3m2﹣3=0,然后由根与系数的关系进行求解.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上. (I)求证:BC⊥平面ACFE;
(II)当EM为何值时,AM∥平面BDF?证明你的结论.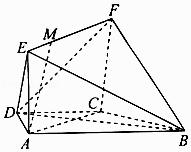
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ), ![]() 的最小正周期为π,且图象关于x=
的最小正周期为π,且图象关于x= ![]() 对称.
对称.
(1)求ω和φ的值;
(2)将函数f(x)的图象上所有横坐标伸长到原来的4倍,再向右平移 ![]() 个单位得到函数g(x)的图象,求g(x)的单调递增区间以及g(x)≥1的x取值范围.
个单位得到函数g(x)的图象,求g(x)的单调递增区间以及g(x)≥1的x取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax2﹣2(a+1)x+3(a∈R).
(1)若函数f(x)在 ![]() 单调递减,求实数a的取值范围;
单调递减,求实数a的取值范围;
(2)令h(x)= ![]() ,若存在
,若存在 ![]() ,使得|h(x1)﹣h(x2)|≥
,使得|h(x1)﹣h(x2)|≥ ![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若抛物线y2=2px上恒有关于直线x+y﹣1=0对称的两点A,B,则p的取值范围是( )
A.(﹣ ![]() ,0)
,0)
B.(0, ![]() )
)
C.(0, ![]() )
)
D.(﹣∞,0)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,给出以下结论: ①直线A1B与B1C所成的角为60°;
②若M是线段AC1上的动点,则直线CM与平面BC1D所成角的正弦值的取值范围是 ![]() ;
;
③若P,Q是线段AC上的动点,且PQ=1,则四面体B1D1PQ的体积恒为 ![]() .
.
其中,正确结论的个数是( )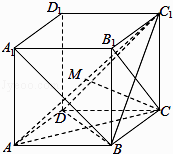
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=4sinx(cosx﹣sinx)+3 (Ⅰ)当x∈(0,π)时,求f(x)的单调递减区间;
(Ⅱ)若f(x)在[0,θ]上的值域为[0,2 ![]() +1],求cos2θ的值.
+1],求cos2θ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com