
已知动点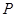 ,Q都在曲线C:
,Q都在曲线C: (β为参数)上,对应参数分别为
(β为参数)上,对应参数分别为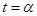
与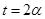 (0<
(0<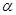 <2π),M为PQ的中点。
<2π),M为PQ的中点。
(Ⅰ)求M的轨迹的参数方程
(Ⅱ)将M到坐标原点的距离d表示为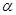 的函数,并判断M的轨迹是否过坐标原点。
的函数,并判断M的轨迹是否过坐标原点。
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| |MQ| |
| 1 |
| |NQ| |
查看答案和解析>>
科目:高中数学 来源:2013年全国统一高考数学试卷(文科)(新课标Ⅱ)(解析版) 题型:解答题
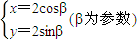 上,对应参数分别为β=α与β=2α(0<α<2π),M为PQ的中点.
上,对应参数分别为β=α与β=2α(0<α<2π),M为PQ的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
选修4-4:坐标系与参数方程
已知动点P. Q都在曲线C:![]() (t为参数)上,对应参数分别为t=a与t=2a(0<a<2π),M为PQ的中点。
(t为参数)上,对应参数分别为t=a与t=2a(0<a<2π),M为PQ的中点。
(I)求M的轨迹的今数方程:
(Ⅱ)将M到坐标原点的距离d表示为a的26数,并判断M的轨迹是否过坐标原点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com