
(12分)
已知向量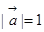 ,
, ,
,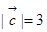 ,且
,且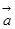 ,
,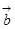 ,
,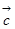 两两的夹角都是
两两的夹角都是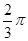 ,
,
求:(1)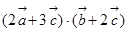 ;
;
(2)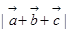 ;
;
(3)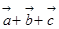 与
与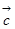 所成的夹角。
所成的夹角。
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源:2011-2012学年山西省大同市高三第三次月考理科数学 题型:解答题
(本小题满分12分)
已知函数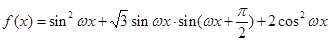 ,
,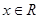 ,
,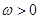 ,在y轴右侧的第一个最高点的横坐标为
,在y轴右侧的第一个最高点的横坐标为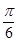 .
.
(1) 求ω;
(2) 若将函数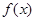 的图象向右平移
的图象向右平移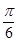 个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数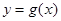 的图象,求函数
的图象,求函数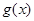 的最大值及单调递减区间.
的最大值及单调递减区间.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年大纲版高三上学期单元测试(3)数学试卷 题型:解答题
(本小题满分12分)
已知直线l上有一列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,其中n∈N*,x1=1,x2=2,点Pn+2分有向线段 所成的比为λ(λ≠-1).
所成的比为λ(λ≠-1).
(1)写出xn+2与xn+1,xn之间的关系式;
(2)设an=xn+1-xn,求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源:2011年江苏省高一上学期期末考试数学试卷 题型:解答题
(本小题12分)
已知 ,
, ,当
,当 为何值时,
为何值时,
(1)  与
与 垂直?
垂直?
(2) 
 与
与
 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高二上学期期末考试数学理卷 题型:解答题
(本小题满分12分)
已知直线 过抛物线
过抛物线 的焦点
的焦点 且与抛物线相交于两点
且与抛物线相交于两点 ,自
,自 向准线
向准线 作垂线,垂足分别为
作垂线,垂足分别为 .
.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)证明:无论 取何实数时,
取何实数时, ,
, 都是定值;
都是定值;
 (III)记
(III)记 的面积分别为
的面积分别为 ,试判断
,试判断 是否成立,并证明你的结论.
是否成立,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2010-2011年湖北省沙市高一上学期期末考试数学文卷 题型:解答题
(本题12分)
已知
①
求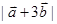 ;
;
②当k为何实数时,k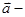
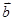 与
与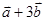 平行, 平行时它们是同向还是反向?
平行, 平行时它们是同向还是反向?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com