
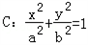 (a>b>0)经过点
(a>b>0)经过点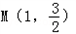 ,其离心率为
,其离心率为 .
.解:(Ⅰ)由已知,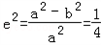 ,所以3a2=4b2,①
,所以3a2=4b2,①
又点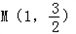 在椭圆C上,所以
在椭圆C上,所以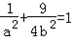 ,②
,②
由①②解之,得a2=4,b2=3.故椭圆C的方程为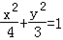 .
.
(Ⅱ)当直线l有斜率时,设y=kx+m时,则由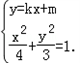
消去y得,(3+4k2)x2+8kmx+4m2﹣12=0,
△=64k2m2﹣4(3+4k2)(4m2﹣12)=48(3+4k2﹣m2)>0,
③设A、B、P点的坐标分别为(x1,y1)、(x2,y2)、(x0,y0),则: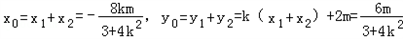 ,
,
由于点P在椭圆C上,所以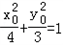 .从而
.从而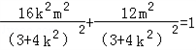 ,
,
化简得4m2=3+4k2,经检验满足③式.
又点O到直线l的距离为: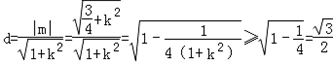 .
.
当且仅当k=0时等号成立,当直线l无斜率时,由对称性知,点P一定在x轴上,
从而P点为(﹣2,0),(2,0),直线l为x=±1,
所以点O到直线l的距离为1,O到直线l的距离最小值为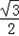 .
.


科目:高中数学 来源: 题型:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源:2014届广东省、阳东一中高二上联考文数试卷(解析版) 题型:解答题
(本题满分14分)
如图,已知椭圆 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.

(1)若∠F1AB=90°,求椭圆的离心率;
(2)若 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试文科数学(天津卷解析版) 题型:解答题
已知椭圆 (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。
(I)求椭圆的离心率。
(II)设A为椭圆的右顶点,O为坐标原点,若Q在椭圆上且满足|AQ|=|AO|,求直线OQ的斜率的值。
【考点定位】本小题主要考查椭圆的标准方程和几何性质、直线的方程、平面内两点间距离公式等基础知识. 考查用代数方法研究圆锥曲线的性质,以及数形结合的数学思想方法.考查运算求解能力、综合分析和解决问题的能力.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省天门市高三天5月模拟文科数学试题 题型:解答题
已知椭圆 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
(1)求椭圆C的标准方程;
(2)当椭圆C的右焦点F在以AB为直径的圆内时,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010年河北省邯郸市高二上学期期末考试数学理卷 题型:解答题
(本小题满分 分)
分)
(普通高中)已知椭圆 (a>b>0)的离心率
(a>b>0)的离心率 ,焦距是函数
,焦距是函数 的零点.
的零点.
(1)求椭圆的方程;
(2)若直线 与椭圆交于
与椭圆交于 、
、 两点,
两点, ,求k的值.
,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com