
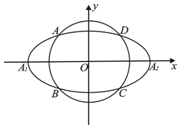
 ��ͼ����ԲC0��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��a��bΪ����������ԲC1��x2+y2=t12��b��t1��a������A1��A2�ֱ�ΪC0�����Ҷ��㣬C1��C0�ཻ��A��B��C��D�ĵ㣮
��ͼ����ԲC0��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��a��bΪ����������ԲC1��x2+y2=t12��b��t1��a������A1��A2�ֱ�ΪC0�����Ҷ��㣬C1��C0�ཻ��A��B��C��D�ĵ㣮���� ��1�����DF1F2=�ȣ���DF2=2csin�ȣ�DF1=2ccos�ȣ�����|DF1|+|DF2|=2a���õ�2ccos��+2csin��=2a��Ȼ������DOC=$4��=\frac{��}{3}$��
��2����$A��{{x_0}��{y_0}}����{A^/}��{{x_1}��{y_1}}��$������ABCD�����A��B��C��D�������ֱ�ΪS��S�䣬�����Բ�ķ��̣��������ı���ʽ������t12+t22=a2+b2���Ƴ�$��{{x_0}^2+{x_1}^2}����{1-\frac{b^2}{a^2}}��+{b^2}-{a^2}=0$��Ȼ���Ƴ�S=S�䣬���ɵõ�����ABCD�����A��B��C��D��������ȣ�
��� �⣺��1�����DF1F2=�ȣ���DF2=2csin�ȣ�DF1=2ccos�ȡ���1�֣�
��|DF1|+|DF2|=2a��2ccos��+2csin��=2a����2�֣�
��$\sqrt{2}sin��{��+\frac{��}{4}}��=\frac{a}{c}$����3�֣�
�����⣬$\frac{c}{a}=\frac{{\sqrt{6}}}{3}$����$sin��{��+\frac{��}{4}}��=\frac{{\sqrt{3}}}{2}$��$��=\frac{��}{12}$����4�֣�
�ʡ�DOC=$4��=\frac{��}{3}$������5�֣�
��2����$A��{{x_0}��{y_0}}����{A^/}��{{x_1}��{y_1}}��$������ABCD�����A��B��C��D�������ֱ�ΪS��S��
��${x_0}^2+{y_0}^2={t_1}^2��{x_1}^2+{y_1}^2={t_2}^2$��$S=4|{x_0}|•|{y_0}|��{S^/}=4|{x_1}|•|{y_1}|$����6�֣�
��${t_1}^2+{t_2}^2={a^2}+{b^2}$����${x_0}^2+{y_0}^2+{x_1}^2+{y_1}^2={a^2}+{b^2}$����7�֣�
��${y_0}^2={b^2}��{1-\frac{{{x_0}^2}}{a^2}}��$��${y_1}^2={b^2}��{1-\frac{{{x_1}^2}}{a^2}}��$��
��${x_0}^2+{b^2}��{1-\frac{{{x_0}^2}}{a^2}}��+{x_1}^2+{b^2}��{1-\frac{{{x_1}^2}}{a^2}}��={a^2}+{b^2}$����8�֣�
��$��{{x_0}^2+{x_1}^2}����{1-\frac{b^2}{a^2}}��+{b^2}-{a^2}=0$��
��$��{\frac{{{x_0}^2+{x_1}^2}}{a^2}-1}����{{a^2}-{b^2}}��=0$��
��a��b��$\frac{{{x_0}^2+{x_1}^2}}{a^2}=0$����${x_0}^2+{x_1}^2={a^2}$����9�֣�
��${S^2}-{S^{/2}}=16��{{x_0}^2{y_0}^2-{x_1}^2{y_1}^2}��$����10�֣�
=$16[{{x_0}^2•{b^2}��{1-\frac{{{x_0}^2}}{a^2}}��-{x_1}^2•{b^2}��{1-\frac{{{x_1}^2}}{a^2}}��}]$
=$16{b^2}��{{x_0}^2-{x_1}^2-\frac{{{x_0}^4}}{a^2}+\frac{{{x_1}^4}}{a^2}}��$����11�֣�
=$16{b^2}��{{x_0}^2-{x_1}^2}����{1-\frac{{{x_0}^2+{x_1}^2}}{a^2}}��$=0��
��S=S�䣬������ABCD�����A��B��C��D��������ȣ�����12�֣�
���� ���⿼��ֱ������Բ��λ�ù�ϵ��Ӧ�ã���������Լ�ת��˼���Ӧ�ã��������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12 | B�� | 56 | C�� | 256 | D�� | 306 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��ͼ��������SABC�IJ����Ϊ$48\sqrt{3}$��OΪ������������ABC�����ģ�
��֪��ͼ��������SABC�IJ����Ϊ$48\sqrt{3}$��OΪ������������ABC�����ģ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
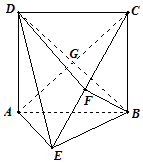 ��ͼ������ABCD�У�AD��ƽ��ABE��AE=EB=BC=2��FΪCE�ϵĵ㣬��BF��ƽ��ACE��BD��AC=G��
��ͼ������ABCD�У�AD��ƽ��ABE��AE=EB=BC=2��FΪCE�ϵĵ㣬��BF��ƽ��ACE��BD��AC=G���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com