Question

考察下列每组对象能否构成一个集合？

(1)美丽的小鸟；

(2)不超过20的非负数；

(3)3、x、x²这三个实数.

Answer 1

解：(1)“美丽的小鸟”无明确标准，对于某个小鸟是否是“美丽的”无法给出明确的判断，即元素不具备确定性，因此(1)不能构成集合；

(2)任给一个实数x,可以明确地判断是不是“不超过20的非负数”，即“0≤x≤20”与“x<0或x>20”.两者必居其一，且仅居其一，故(2)能构成集合.

(3)虽然三个实数已被指定，但这三个实数却不一定能构成集合，因为3、x、x²之间有可能相等，所以不一定满足元素的互异性.如果添加条件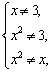即x≠3且x≠±且x≠0且x≠1，那么三个实数3、x、x²就可以构成一个集合.

点评：集合中的元素一定具有确定性、互异性、无序性；反过来，一组对象若不具备这三个特性，则这组对象也就不能构成集合.因此，在分析、处理集合问题的过程中，要时刻注意集合元素的三个特征对集合元素的限制.