
分析 先求函数f(x)的导数,然后令f′(x0)=1,求出x0的值后再求其正切值即可.
解答 解:∵f(x)=$\frac{1}{2}$x-$\frac{1}{4}$sinx-$\frac{\sqrt{3}}{4}$cosx
∴f′(x)=$\frac{1}{2}$-$\frac{1}{4}$cosx+$\frac{\sqrt{3}}{4}$sinx=$\frac{1}{2}$+$\frac{1}{2}$sin(x-$\frac{π}{6}$)
又因为f′(x0)=$\frac{1}{2}$+$\frac{1}{2}$sin(x0-$\frac{π}{6}$)=$\frac{1}{2}$,
∴sin(x0-$\frac{π}{6}$)=0,x0=$\frac{π}{6}$+2kπ (k∈Z);x0=$2kπ+\frac{5π}{6}$,(k∈Z).
∴tanx0=$±\frac{\sqrt{3}}{3}$.
故答案为:$±\frac{\sqrt{3}}{3}$.
点评 本题主要考查导数的几何意义,即函数在某点的导数值等于在该点处切线的斜率.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,0) | B. | (-2,0) | C. | (-1,0) | D. | (1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | φ=$\frac{π}{4}$是f(x)=3in(x-2φ)的图象关于y轴对称的充分不必要条件 | |
| B. | |$\overrightarrow{a}$|-|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|的充要条件是$\overrightarrow{a}$与$\overrightarrow{b}$方向相同 | |
| C. | a,b,c都为实数,b=$\sqrt{ac}$是a,b,c三数成等比数列的充分不必要条件 | |
| D. | m=3是直线(m+3)x+my-2=0与mx-6y+5=0互相垂直的充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
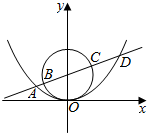 如图所示,过抛物线x2=4py(p>0)焦点的直线依次交抛物线与圆x2+(y-p)2=p2于点A,B,C,D,则$\overrightarrow{AB}$•$\overrightarrow{CD}$的值是( )
如图所示,过抛物线x2=4py(p>0)焦点的直线依次交抛物线与圆x2+(y-p)2=p2于点A,B,C,D,则$\overrightarrow{AB}$•$\overrightarrow{CD}$的值是( )| A. | 8p2 | B. | 4p2 | C. | 2p2 | D. | p2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com