解:(1)由题意可得,当x<1时,f′(x)=-3x
2+2x+b,f′(-1)=-3-2+b=b-5.
由( b-5 )(

)=-1,可得b=0,故 f(x)=-x
3+x
2+c.
把点(-1,2)代入求得 c=0.
综上可得b=0,c=0.
(2)由以上可得
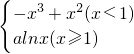
,当-1≤x<1时,f′(x)=-x(3x-2).
解f′(x)>0得0<x<

.解f′(x)<0得1≥x>

或x<0.
∴f(x)在(-1,0)和(

,1)上单调递减,在(0,

)上单调递增,
从而f(x)在x=

处取得极大值为f(

)=

.
又∵f(-1)=2,f(1)=0,∴f(x)在[-1,1)上的最大值为2.
当1≤x≤e时,f(x)=alnx,当a≤0时,f(x)≤0.
当a>0时,f(x)在[1,e]单调递增;∴f(x)在[1,e]上的最大值为a.
∴a≥2时,f(x)在[-1,e]上的最大值为a;当a<2时,f(x)在[-1,e]上的最大值为2.
(3)设点P的横坐标为m(不妨设m>0),则由题意可得点Q的横坐标为-m,且-m<0.
当0<m<1时,点P(m,-m
3+m
2),点 Q(-m,m
3+m
2),由K
0P•K
OQ=-1,可得
(-m
2+m)(-m
2-m)=-1,m无解.
当m≥1时,点P(m,alnm),点 Q(-m,m
3+m
2),由K
0P•K
OQ=-1,可得
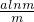
•(-m
2-m)=-1,即 alnm=
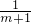
.由于a为正实数,故存在大于1的实数m,满足方程 alnm=
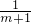
.
故曲线y=f(x)上存在两点P,Q,使得△POQ是以O为直角顶点的直角三角形,且此三角形斜边中点在y轴上.
分析:(1)求出x<1时的导函数,令f(-1)=2,f′(x)=-5,解方程组,求出b,c的值.
(2)分段求函数的最大值,利用导数先求出-1≤x<1时的最大值;再通过对a的讨论,判断出1≤x≤e时函数的
单调性,求出最大值,再从两段中的最大值选出最大值.
(3)设点P的横坐标为m(不妨设m>0),则由题意可得点Q的横坐标为-m,且-m<0.由题意可得OP⊥OQ,
即K
0P•K
OQ=-1.分0<m<1和m≥1两种情况,分别检验,从而得出结论.
点评:本题主要考查利用导数研究函数的单调性,曲线对应的函数在切点处的导数值为切线的斜率;求分段函数的性质时应该分段去求体现了分类讨论和等价转化的数学思想,属于难题.

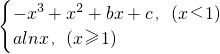 的图象过点(-1,2),且在点(-1,f(-1))处的切线与直线x-5y+1=0垂直.
的图象过点(-1,2),且在点(-1,f(-1))处的切线与直线x-5y+1=0垂直. )=-1,可得b=0,故 f(x)=-x3+x2+c.
)=-1,可得b=0,故 f(x)=-x3+x2+c.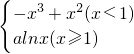 ,当-1≤x<1时,f′(x)=-x(3x-2).
,当-1≤x<1时,f′(x)=-x(3x-2). .解f′(x)<0得1≥x>
.解f′(x)<0得1≥x> 或x<0.
或x<0. ,1)上单调递减,在(0,
,1)上单调递减,在(0, )上单调递增,
)上单调递增, 处取得极大值为f(
处取得极大值为f( )=
)= .
.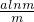 •(-m2-m)=-1,即 alnm=
•(-m2-m)=-1,即 alnm=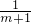 .由于a为正实数,故存在大于1的实数m,满足方程 alnm=
.由于a为正实数,故存在大于1的实数m,满足方程 alnm=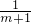 .
.

 阅读快车系列答案
阅读快车系列答案