
 “5•12”汶川大地震是华人心中永远的痛!在灾后重建中拟在矩形区域ABCD内建一矩形(与原方位一样)的汶川人民纪念广场(如图),另外AEF内部有一废墟作为文物保护区不能占用,经测量AB=100m,BC=80m,AE=30m,AF=20m,如何设计才能使广场面积最大?
“5•12”汶川大地震是华人心中永远的痛!在灾后重建中拟在矩形区域ABCD内建一矩形(与原方位一样)的汶川人民纪念广场(如图),另外AEF内部有一废墟作为文物保护区不能占用,经测量AB=100m,BC=80m,AE=30m,AF=20m,如何设计才能使广场面积最大?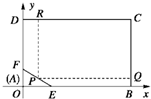 解:建立如图所示的直角坐标系,则E(30,0),F(0,20),
解:建立如图所示的直角坐标系,则E(30,0),F(0,20),| x |
| 30 |
| y |
| 20 |
| m |
| 30 |
| n |
| 20 |
| m |
| 30 |
| 2m |
| 3 |
| 2 |
| 3 |
| 18050 |
| 3 |
| |EP| |
| |PF| |
| 30-5 |
| 5 |
| 5 |
| 1 |


科目:高中数学 来源: 题型:
 “5•12”汶川大地震中,受灾面积大,伤亡惨重,医疗队到达后,都会选择一个合理的位置,使伤员能在最短的时间内得到救治.设有三个乡镇,分别位于一个矩形ABCD的两个顶点A,B及CD的中点P处,AB=10km,BC=5km,现要在该矩形的区域内(含边界),且与A,B等距离的一点O处建造一个医疗站,记O点到三个乡镇的距离之和为y.
“5•12”汶川大地震中,受灾面积大,伤亡惨重,医疗队到达后,都会选择一个合理的位置,使伤员能在最短的时间内得到救治.设有三个乡镇,分别位于一个矩形ABCD的两个顶点A,B及CD的中点P处,AB=10km,BC=5km,现要在该矩形的区域内(含边界),且与A,B等距离的一点O处建造一个医疗站,记O点到三个乡镇的距离之和为y.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 “5•12”汶川大地震中,受灾面积大,伤亡惨重,医疗队到达后,都会选择一个合理的位置,使伤员能在最短的时间内得到救治.设有三个乡镇,分别位于一个矩形ABCD的两个顶点A,B及CD的中点P处,AB=10km,BC=5km,现要在该矩形的区域内(含边界),且与A,B等距离的一点O处建造一个医疗站,记O点到三个乡镇的距离之和为y.
“5•12”汶川大地震中,受灾面积大,伤亡惨重,医疗队到达后,都会选择一个合理的位置,使伤员能在最短的时间内得到救治.设有三个乡镇,分别位于一个矩形ABCD的两个顶点A,B及CD的中点P处,AB=10km,BC=5km,现要在该矩形的区域内(含边界),且与A,B等距离的一点O处建造一个医疗站,记O点到三个乡镇的距离之和为y.查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省黄冈中学、鄂南中学高一(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com