
在航天员进行的一项太空实验中,要先后实施6个程序,其中程序A只能出现在第一步或最后一步,程序B和C在实施时必须相邻,则在该实验中程序顺序的编排方法共有( )
A.144种 B.96种 C.48种 D.34种
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源:2015-2016学年河北省高二上学期期中数学试卷(解析版) 题型:选择题
已知双曲线的一个焦点与抛物线 的焦点重合,且其渐近线方程为
的焦点重合,且其渐近线方程为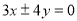 ,则该双曲线的标准方程为
,则该双曲线的标准方程为
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届江西省高三上学期期中文科数学试卷(解析版) 题型:解答题
(本小题满分12分)设向量 ,其中
,其中 ,
, ,已知函数
,已知函数 的最小正周期为
的最小正周期为 .
.
(1)求 的对称中心;
的对称中心;
(2)若 是关于
是关于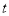 的方程
的方程 的根,且
的根,且 ,求
,求 的值.
的值.
【答案】(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)先利用两角和与差的正弦化简函数的解析式,再根据函数最小正周期求得函数的解析式,由此求得函数的对称中心;(2)先根据方程根的概念求得 的值,再由
的值,再由 的范围求得
的范围求得 的值,从而代入函数解析式中求得
的值,从而代入函数解析式中求得 的值.
的值.
试题解析:(1) 

又  , 得
, 得  所以
所以  对称中心为
对称中心为 
(2)由 得
得  或
或  即
即 或
或 ,又
,又
所以 ,得
,得 ,故
,故
考点:1、两角两角和与差的正弦;2、三角函数的周期;3、特殊三角形函数的值.
【规律点睛】平面向量与三角函数的综合,通常利用平面向量的垂直、平行、数量积公式等知识将向量问题转化为三角函数问题,再结合三角知识求解.而求三角函数的最值(值域)、单调性、奇偶性、对称性,通常要将函数的解析式转化为 的形式,然后利用整体思想求解.
的形式,然后利用整体思想求解.
【题型】解答题
【适用】较难
【标题】【百强校】2016届江西省临川一中高三上学期期中文科数学试卷(带解析)
【关键字标签】
【结束】
(本小题满分12分)在四棱柱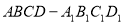 中,
中, ,底面
,底面 为菱形,
为菱形,
 ,已知
,已知 .
.

(1)求证:平面 平面
平面 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源:2016届甘肃省高三上学期期中理科数学试卷(解析版) 题型:选择题
已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.下列说法中正确的是( )
A.f(0)f(1)>0 B.f(0)f(3)>0
C.f(0)f(2)>0 D.f(0)f(3)<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com