

图3-3-13
求飞标落在阴影部分的概率.
|
思路分析:几何概型问题一般有公式法和随机模拟两种方法,当然随机模拟方法比较麻烦,
在公式法不好进行的情况下可考虑随机模拟方法. 我们分别用两种方法计算该事件的概率: (1)利用几何概型的公式; (2)用随机模拟的方法. 解:方法一:由于随机地投掷飞标,飞标落在正方形内每一个点的机会是等可能的,所以符合几何概型的条件. S阴影= ∴P= 方法二:通过建立坐标系,得到两“长度”曲线的范围,才能对随机变量进行平移、伸缩变换,只有得到两“长度”曲线的方程,才能数出适合条件的数组数. (1)利用计算器或计算机产生两组0至1区间内的均匀随机数a1、b1(共N组); (2)经平移和伸缩变换,a=(a1-0.5)*2,b=(b1-0.5)*2; (3)数出满足不等式b<2a- 所求概率P≈ |


科目:高中数学 来源:广东省09-10学年高二下学期期末考试数学试题(文科卷) 题型:解答题
(满分13分)如图所示,将一个圆形的画板分成面积相等的三部分,
每部分上分别涂色为黄、红、蓝三色,某人随机向画板投射一只镖,
如果射中边界则重新再射,射中涂色部分则分别得分为3,2, 1分,
投射两次的得分为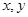 ,记
,记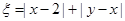 .
.
求随机变量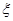 的最大值,并求事件“
的最大值,并求事件“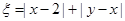 取得最大值”的概率.
取得最大值”的概率.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com