
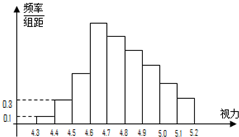
 为了解某校高二学生的视力情况,随机地抽查了该校100名高二学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为B,视力在4.6到5.0之间的学生数为F.
为了解某校高二学生的视力情况,随机地抽查了该校100名高二学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为B,视力在4.6到5.0之间的学生数为F.| 21 |
| 45 |
| 7 |
| 15 |
| 7 |
| 15 |


科目:高中数学 来源:山西省忻州一中2011-2012学年高二上学期期中考试数学文科试题 题型:022
为了解某校高中学生的近视眼发病率,在该校学生分层抽样调查,高一、高二、高三分别有学生800名,600名,500名.若高三学生共抽取25名,则高一年级每位学生被抽到的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
为了解某校高中学生的视力情况,对该校学生按年级进行分层抽样调查,已知该校高一、高二、高三分别有学生800名、600名、500名,若高三学生共被抽取25名,则高一年级应被抽取的学生数为 .
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省高三上学期第一次月考文科数学 题型:填空题
为了解某校高中学生的近视眼发病率,在该校学生分层抽样调查,高一、高二、
高三分别有学生800名,600名,500名。若高三学生共抽取25名,则高一年级每位学生被
抽到的概率为 .
查看答案和解析>>
科目:高中数学 来源:2010年吉林省高三第五次模拟考试数学(理科)试题 题型:填空题
为了解某校高中学生的近视眼发病率,在该校学生中进行分层抽样调查,已知该校高一、高二、高三分别有学生 名、
名、 名、
名、 名,若高三学生共抽取
名,若高三学生共抽取 名,则高一年级每一位学生被抽到的概率是___________.
名,则高一年级每一位学生被抽到的概率是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com