Question

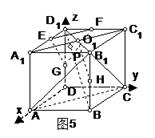
如图5：正方体ABCD-A₁B₁C₁D₁，过线段BD₁上一点P（P平面ACB₁）作垂直于D₁B的平面分别交过D₁的三条棱于E、F、G．

(1)求证：平面EFG∥平面A CB₁，并判断三角形类型；

(2)若正方体棱长为a，求△EFG的最大面积，并求此时EF与B₁C的距离．

Answer 1

（1）见解析（2）·a

解析:

(证明（1）用纯粹的几何方法要辗转证明EF∥AC，EG∥B₁C，FG∥AB₁来证明，而我们借用向量法使问题代数化，运算简洁，思路简单明了．)

(1)分析：要证平面EFG平面ACB₁，由题设知只要证BD₁垂直平面ACB₁即可．

证明：以D为坐标原点，建立空间直角坐标系，如图5，不妨设正方体棱长为a，则A（a，0，0），B（a，a，0），C（0，a，0），D₁（0，0，a），B₁（a，a，a），E（x_E，0，a），F（0，y_F，a），G（0，0，z_G）．

∴=（－a，－a，a），=（0，a，a），（－x_E，y_F，0），=（－a，a，0），=（－a，0，－a），

∵·=(－a，－a，a)·(0，a，a)=0，

∴⊥ ，

同理 ⊥，

而与不共线且相交于点A，

∴⊥平面ACB₁，又已知⊥平面EFG，

∴ 平面EFG∥平面ACB₁；

又因为⊥平面EFG，所以 ⊥，

则·=0， 

即 (－a，－a，a)·(－x_E，y_F，0)=0，

化简得  x_E－y_F=0；

同理    x_E－z_G=0,  y_F－z_G=0，

易得   ==，

 ∴  △EFG为正三角形．

(2)解：因为△EFG是正三角形，显然当△EFG与△A₁C₁D重合时，△EFG的边最长，其面积也最大，此时，=A₁C₁=·a，

 ∴=

         = ·sin60⁰

         = (·a)2·

         =·a2  ．

此时EF与B₁C的距离即为A₁C₁与B₁C的距离，由于两异面直线所在平面平行，所求距离转化为求点B₁到平面 A₁C₁D的距离，记A₁C₁与B₁D₁交于点O₁，作O₁H∥D₁B并交BB₁于点H，则O₁H⊥平面A₁C₁D，垂足为O₁，则O₁(，，a)，H(a，a，)，而作为平面A₁C₁D的法向量，

所以异面直线EF与B₁C的距离设为d是

d = ==·a．

(证明（2）时一般要找到求这两平面距离的两点，如图5*，而这两点为K与J，在立体图形中较难确定，且较难想到通过作辅助线DO₁，OB₁来得到，加上在如此复杂的空间图形中容易思维混乱，但只要借助平面法向量求线段的射影长度的思想，结合题设，使思路清晰明了，最终使问题的解决明朗化；把握这种思想，不管是空间线线距离，线面距离，面面距离问题，一般我们都能转化成点线或点面距离，再借助平面法向量很好地解决了．)