Question

 长沙市某棚户区改造建筑用地平面示意图如图所示．经规划调研确定，棚改规划建筑用地区域近似地为半径是R的圆面．该圆面的内接四边形ABCD是原棚户建筑用地，测量可知边界AB = AD = 4万米，BC = 6万米，CD = 2万米．

（1）请计算原棚户区建筑用地ABCD的面积及圆面的半径R的值；

（2）因地理条件的限制，边界AD、DC不能变更，而边界AB、BC可以调整，为了提高棚户区改造建筑用地的利用率，请在圆弧上设计一点P；使得棚户区改造的新建筑用地APCD的面积最大，并求最大值．

 

 

 

 

 

 

 

 

 

Answer 1

【答案】

 【解析】（1）因为四边形ABCD内接于圆，所以∠ABC    +∠ADC = 180°，连接AC，由余弦定理：

AC² = 4² + 6² – 2×4×6×cos∠ABC = 4² + 2² – 2×2×4 cos∠ADC．

所以cos∠ABC =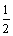，∵∠ABC∈(0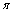，)，故∠ABC = 60°．

S_{四边形ABCD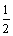} = ×4×6×sin60°+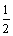×2×4×sin120°= 8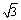（万平方米）．………………4分

在△ABC中，由余弦定理：

AC² = AB² + BC ²– 2AB·BC·cos∠ABC

   = 16 + 36 – 2×4×6×．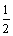

   AC = 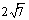．…………………………6分

由正弦定理，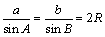

∴

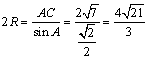
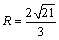∴（万米）．………………8分

（2）∵S_{四边形APCD} = S_△ADC + S_△APC

又S_△ADC = 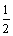AD·CD·sin120°= 2，

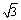设AP = x， CP = y．

则S_△APC = 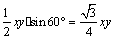．……………………10分

又由余弦定理AC² = x² + y² – 2xy cos60°

= x² + y² – xy

= 28．

∴x² + y² – xy≥2xy – xy = xy．

∴xy≤28     当且仅当x = y时取等号……………………12分

∴S_{四边形APCD} = 2+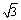

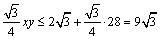
∴最大面积为9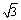万平方米．…………………………13分．