
| 2 | 3 |
| 2 |
| 3 |
| ||||
|
| 1 |
| 5 |
| ||||
|
| 3 |
| 5 |
| ||||
|
| 1 |
| 5 |

| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |


科目:高中数学 来源:2014届浙江省高二下期末考试理科数学试卷(解析版) 题型:解答题
某单位为了参加上级组织的普及消防知识竞赛,需要从两名选手中选出一人参加.为此,设计了一个挑选方案:选手从6道备选题中一次性随机抽取3题.通过考察得知:6道备选题中选手甲有4道题能够答对,2道题答错;选手乙答对每题的概率都是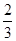 ,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.
,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.
(1)写出ξ的概率分布列,并求出E(ξ),E(η);
(2)求D(ξ),D(η).请你根据得到的数据,建议该单位派哪个选手参加竞赛?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.
,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省宁波市余姚中学高二(下)期中数学试卷(理科)(解析版) 题型:解答题
 ,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.
,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省宁波市万里国际学校高二(下)期末数学试卷(理科)(解析版) 题型:解答题
 ,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.
,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com