练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在
    a
    =“向北走20km”，
    b
    =“向西走15km”，则|
    a
    -
    b
    |    =
     
    ，
    a
    +
    b
    与
    a
    的夹角的余弦值=
     
    ．
    分析：利用向量垂直的充要条件求出
    a
    •
    b
    ；利用向量模的平方等于向量的平方求出向量的模；利用向量的数量积公式求向量的夹角余弦．
    解答：解：∵
    a
    =“向北走20km”，
    b
    =“向西走15km”，
    ∴|
    a
    |=20，  |
    b
    |=15     
    a
    ⊥
    b

    |
    a
    -
    b
    |=
    a
    2    -2
    a
    •
    b
    +
    b
    2
    =25
    |
    a
    +
    b
    |=
    a
    2    +2
    a
    •
    b
    +
    b
    2
    =25
    (
    a
    +
    b
    )•
    a
    =
    a
    2    +
    a
    •
    b
    =400
    ∴
    a
    +
    b
    与
    a
    的夹角的余弦值=
    (
    a
    +
    b
    )•
    a
    |
    a
    +
    b
    |•
    a
     |
    =
    4
    5

    故答案为：25km，
    4
    5
    点评：本题考查求向量模的方法是将模平方，利用向量模的平方等于向量的平方；考查向量的数量积公式求向量的夹角．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：福建省厦门六中2011－2012学年高一下学期期中考试数学试题 题型：044

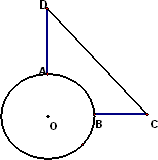
    如图所示，福建某土楼占地呈圆域形状，O为土楼中心，半径为40 m，它的斜对面有一条公路，从土楼东门B向东走260 m到达公路边的C点，从土楼北门A向北走360 m到达公路边的D点，现准备在土楼的边界选一点E修建一条由E通往公路CD的便道，要求造价最低(最短距离)，用坐标法回答E点应该选在何处．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若a=“向北走8 km”，b=“向东走8 km”，则|a+b|=__________；a+b的方向是___________.

    查看答案和解析>>

    科目：高中数学 来源：2014届福建省高一下学期期中数学试卷（解析版） 题型：解答题

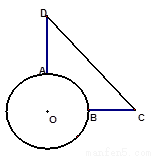
    如图所示，福建某土楼占地呈圆域形状，O为土楼中心，半径为40m，它的斜对面有一条公路，从土楼东门B向东走260 m到达公路边的C点，从土楼北门A向北走360 m到达公路边的D点，现准备在土楼的边界选一点E修建一条由E通往公路CD的便道，要求造价最低(最短距离)，用坐标法回答E点应该选在何处。

     

    查看答案和解析>>

    科目：高中数学 来源：《2.2.2 向量减法运算及其几何意义》2011年同步练习（解析版） 题型：填空题

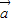    在=“向北走20km”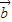，=“向西走15km”，则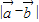=   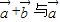 ，的夹角的余弦值=    ．

    查看答案和解析>>

    同步练习册答案