
在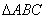 中,内角
中,内角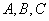 所对的边长分别是
所对的边长分别是 .
.
(1)若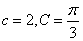 ,且
,且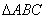 的面积为
的面积为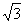 ,求
,求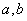 的值;
的值;
(2)若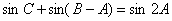 ,试判断
,试判断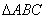 的形状.
的形状.
解:(1)∵c=2,C= ,
,
∴由余弦定理c2=a2+b2-2abcos C 得a2+b2-ab=4.
又∵△ABC的面积为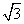 , ∴
, ∴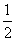 absin C=
absin C=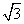 ,ab=4.
,ab=4.
联立方程组 解得a=2,b=2. (4分)
解得a=2,b=2. (4分)
(2)由sin C+sin(B-A)=sin 2A,
得sin(A+B)+sin(B-A)=2sin Acos A,
即2sin Bcos A=2sin Acos A,
∴cos A·(sin A-sin B)=0,
∴cos A=0或sin A-sin B=0,
当cos A=0时,∵0<A<π,
∴A=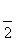 ,△ABC为直角三角形;
,△ABC为直角三角形;
当sin A-sin B=0时,得sin B=sin A,
由正弦定理得a=b,
即△ABC为等腰三角形.
∴△ABC为等腰三角形或直角三角形.(8分)


科目:高中数学 来源: 题型:
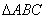 中,角
中,角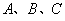 所对的边分别为
所对的边分别为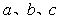 ,下列命题正确的是________(写出正确命题的编号).
,下列命题正确的是________(写出正确命题的编号).
①总存在某内角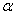 ,使
,使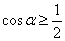 ;
;
②若 ,则
,则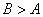 ;
;
③存在某钝角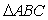 ,有
,有 ;
;
④若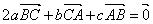 ,则
,则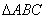 的最小角小于
的最小角小于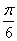 ;
;
⑤若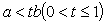 ,则
,则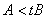 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com