
 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,现有以下结论:①B,D两点间的距离为$\sqrt{3}$;②AD是该圆的一条直径;③CD=$\frac{\sqrt{3}}{2}$;④四边形ABCD的面积S=$\frac{3\sqrt{3}}{4}$.其中正确结论的个数为( )
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,现有以下结论:①B,D两点间的距离为$\sqrt{3}$;②AD是该圆的一条直径;③CD=$\frac{\sqrt{3}}{2}$;④四边形ABCD的面积S=$\frac{3\sqrt{3}}{4}$.其中正确结论的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 在①中,由余弦定理求出BD=$\sqrt{3}$;在②中,由AB⊥BD,知AD是该圆的一条直径;在③中,推导出CD=1;在④中,由四边形是梯形,高为$\frac{\sqrt{3}}{2}$,求出四边形ABCD的面积S=$\frac{3\sqrt{3}}{4}$.
解答 解:在①中,∵∠BCD=120°,∴∠A=60°,
∵AD=2,AB=1,∴BD=$\sqrt{4+1-2×2×1×\frac{1}{2}}$=$\sqrt{3}$,故①正确;
在②中,∵AB⊥BD,∴AD是该圆的一条直径,故②正确;
在③中,3=1+CD2-2CD•(-$\frac{1}{2}$),∴CD2+CD-2=0,∴CD=1,故③不正确;
在④中,由③可得四边形是梯形,高为$\frac{\sqrt{3}}{2}$,四边形ABCD的面积S=$\frac{1+2}{2}•\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{4}$,故④正确.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意圆的性质、余弦定理、梯形性质的合理运用.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,$\frac{1}{2}$) | B. | (-∞,-3)∪($\frac{1}{2}$,+∞) | C. | (-$\frac{1}{2}$,3) | D. | (-∞,-$\frac{1}{2}$)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ①②④ | C. | ①③ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
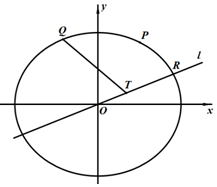 如图,在平面直角坐标系xOy中,点$P(1,\frac{3}{2})$和动点Q(m,n)都在离心率为$\frac{1}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)上,其中m<0,n>0.
如图,在平面直角坐标系xOy中,点$P(1,\frac{3}{2})$和动点Q(m,n)都在离心率为$\frac{1}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)上,其中m<0,n>0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com