
分析 (Ⅰ)根据函数f(x)的图象在点(1,e)处的切线与直线x-(2e+1)y-3=0垂直,求得a,b;
(Ⅱ)由(Ⅰ)得$f(x)=2{e^x}-\frac{lnx}{x}-{e^x}{x^3}$,证f(x)>2,即证2ex-exx3>2$+\frac{lnx}{x}$,构造函数,确定函数的单调性,即可证明结论.
解答 (Ⅰ)解:因为f(1)=e,故(a-b)e=e,故a-b=1①;
依题意,f′(1)=-2e-1;又${f^'}(x)=a{e^x}-\frac{1-lnx}{x^2}-b({e^x}{x^3}+3{x^2}{e^x})$,
故f′(1)=ae-1-4be=-2e-1,故a-4b=-2②,
联立①②解得a=2,b=1,…(5分)
(Ⅱ)证明:由(Ⅰ)得$f(x)=2{e^x}-\frac{lnx}{x}-{e^x}{x^3}$
要证f(x)>2,即证2ex-exx3>2$+\frac{lnx}{x}$; …(7分)
令g(x)=2ex-exx3,∴g′(x)=ex(-x3-3x2+2)=-ex(x3+3x2-2)=-ex(x+1)(x2+2x-2),
故当x∈(0,1)时,-ex<0,x+1>0;
令p(x)=x2+2x-2,因为p(x)的对称轴为x=-1,且p(0)•p(1)<0,
故存在x0∈(0,1),使得p(x0)=0;
故当x∈(0,x0)时,p(x)=x2+2x-2<0,g′(x)=-ex(x+1)(x2+2x-2)>0,
即g(x)在(0,x0)上单调递增;
当x∈(x0,1)时,p(x)=x2+2x-2>0,故g′(x)=-ex(x+1)(x2+2x-2)<0,
即g(x)在(x0,1)上单调递减;因为g(0)=2,g(1)=e,
故当x∈(0,1)时,g(x)>g(0)=2,…(10分)
又当x∈(0,1)时,$\frac{lnx}{x}<0$,∴$2+\frac{lnx}{x}<2$…(11分)
所以2ex-exx3>2$+\frac{lnx}{x}$,即f(x)>2…(12分)
点评 本题考查导数的应用,考查导数的几何意义,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:解答题
 已知A是圆锥的顶点,BD是圆锥底面的直径,C是底面圆周上一点,BD=2,BC=1,AC与底面所成角的大小为$\frac{π}{3}$,过点A作截面ABC,ACD,截去部分后的几何体如图所示.
已知A是圆锥的顶点,BD是圆锥底面的直径,C是底面圆周上一点,BD=2,BC=1,AC与底面所成角的大小为$\frac{π}{3}$,过点A作截面ABC,ACD,截去部分后的几何体如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}+1$ | B. | $\sqrt{3}-1$ | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}+8\sqrt{3}sin(B+\frac{π}{6})$ | B. | $4\sqrt{3}+8sin(B+\frac{π}{3})$ | C. | $4\sqrt{3}+8\sqrt{3}cos(B+\frac{π}{6})$ | D. | $4\sqrt{3}+8cos(B+\frac{π}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
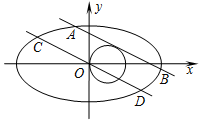 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{{\sqrt{3}}}{2}$,且过点$({2,\sqrt{3}}))$,直线l1:y=kx+m(m>0)与圆C2:(x-1)2+y2=1相切且与椭圆C1交于A,B两点.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{{\sqrt{3}}}{2}$,且过点$({2,\sqrt{3}}))$,直线l1:y=kx+m(m>0)与圆C2:(x-1)2+y2=1相切且与椭圆C1交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 两条直线都和同一个平面平行,则这两条直线平行 | |
| B. | 两条直线没有公共点,则这两条直线平行 | |
| C. | 两条直线都和第三条直线垂直,则这两条直线平行 | |
| D. | 一条直线和一个平面内所有直线没有公共点,则这条直线和这个平面平行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com