
 和2当e=
和2当e= 时圆锥曲线mx2+4y2=4m是椭圆,当e=2时圆锥曲线mx2+4y2=4m是双曲线.由此能够推导出满足条件的圆锥曲线的条数.
时圆锥曲线mx2+4y2=4m是椭圆,当e=2时圆锥曲线mx2+4y2=4m是双曲线.由此能够推导出满足条件的圆锥曲线的条数. 和2
和2 时圆锥曲线mx2+4y2=4m是椭圆,当e=2时圆锥曲线mx2+4y2=4m是双曲线.
时圆锥曲线mx2+4y2=4m是椭圆,当e=2时圆锥曲线mx2+4y2=4m是双曲线.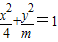 ,
,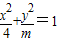 ,是椭圆,则c2=|4-m|,
,是椭圆,则c2=|4-m|,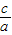 =
=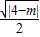 =
= 或
或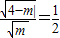 ,满足条件的圆锥曲线有2个;
,满足条件的圆锥曲线有2个;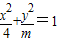 是双曲线,则m<0
是双曲线,则m<0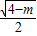 =2,满足条件的圆锥曲线有1个.
=2,满足条件的圆锥曲线有1个.

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com