
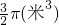 的无盖圆柱形容器,容器的底面半径为r(米),而且制造底面的材料每平方米为30元,制造容器的材料每平方米为20元,设计时材料的厚度可忽略不计.
的无盖圆柱形容器,容器的底面半径为r(米),而且制造底面的材料每平方米为30元,制造容器的材料每平方米为20元,设计时材料的厚度可忽略不计. .
.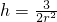
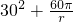 =
=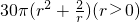
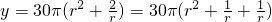
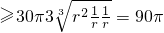
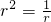 .即r=1时,取等号.
.即r=1时,取等号.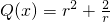 在r∉[2,3]上的单调性.
在r∉[2,3]上的单调性.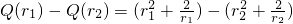 =
=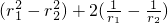 =
=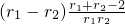 ,
,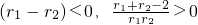 ,
,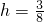 米时,造价最低为465元.
米时,造价最低为465元. 米3,我们设底面半径为r,易求出底面面积,及侧(容器壁)面积,然后再根据制造底面的材料每平方米30元,制造容器壁的材料每平方米20元,我们可得到容器的成本y(元)表示为r的函数的解析式;
米3,我们设底面半径为r,易求出底面面积,及侧(容器壁)面积,然后再根据制造底面的材料每平方米30元,制造容器壁的材料每平方米20元,我们可得到容器的成本y(元)表示为r的函数的解析式;

科目:高中数学 来源: 题型:
| 3 | 2 |
查看答案和解析>>
科目:高中数学 来源:2010年广东省广州一中高三数学二轮复习:不等式2(解析版) 题型:解答题
 的无盖圆柱形容器,容器的底面半径为r(米),而且制造底面的材料每平方米为30元,制造容器的材料每平方米为20元,设计时材料的厚度可忽略不计.
的无盖圆柱形容器,容器的底面半径为r(米),而且制造底面的材料每平方米为30元,制造容器的材料每平方米为20元,设计时材料的厚度可忽略不计.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com