
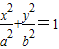 (a>0,b>0)上的两点,则下列四个结论:①a2+b2≥(x+y)2;②
(a>0,b>0)上的两点,则下列四个结论:①a2+b2≥(x+y)2;② ;③
;③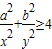 ;④
;④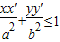 .其中正确的个数为( )
.其中正确的个数为( )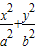 )(a2+b2)替换(a2+b2),
)(a2+b2)替换(a2+b2),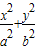 )(
)(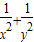 )替换(
)替换(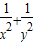 ),再根据柯西不等式(a2+b2)(c2+d2)≥(ac+bd)2可得;
),再根据柯西不等式(a2+b2)(c2+d2)≥(ac+bd)2可得;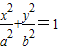 (a>0,b>0)上的点,则
(a>0,b>0)上的点,则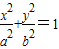 ,
,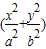 ≥(x+y)2,故①正确;
≥(x+y)2,故①正确;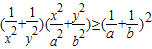 ,故②也正确;
,故②也正确;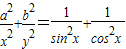 =
=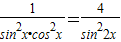 ,显然③也正确;
,显然③也正确; (a>0,b>0)上的点.
(a>0,b>0)上的点. ,故④也正确.
,故④也正确.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| x2 |
| 1 |
| y2 |
| 1 |
| a |
| 1 |
| b |
| a2 |
| x2 |
| b2 |
| y2 |
| xx′ |
| a2 |
| yy′ |
| b2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| x2 |
| 1 |
| y2 |
| 1 |
| a |
| 1 |
| b |
| a2 |
| x2 |
| b2 |
| y2 |
| xx′ |
| a2 |
| yy′ |
| b2 |
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省嘉兴一中高三(上)10月月考数学试卷(文科)(解析版) 题型:选择题
 (a>0,b>0)上的两点,则下列四个结论:①a2+b2≥(x+y)2;②
(a>0,b>0)上的两点,则下列四个结论:①a2+b2≥(x+y)2;② ;③
;③ ;④
;④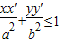 .其中正确的个数为( )
.其中正确的个数为( )查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省温州市瓯海中学高三(上)期中数学试卷(文科)(解析版) 题型:选择题
 (a>0,b>0)上的两点,则下列四个结论:①a2+b2≥(x+y)2;②
(a>0,b>0)上的两点,则下列四个结论:①a2+b2≥(x+y)2;② ;③
;③ ;④
;④ .其中正确的个数为( )
.其中正确的个数为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com