
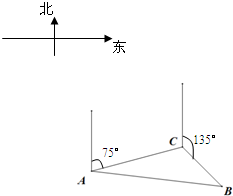
 如图,甲船在A处测得:“乙船位于北偏东75°,距离为10海里的C处,并正沿着北偏东135°的方向,以每小时12海里的速度驶去.”经过半小时,甲船在B处追上了乙船.求:
如图,甲船在A处测得:“乙船位于北偏东75°,距离为10海里的C处,并正沿着北偏东135°的方向,以每小时12海里的速度驶去.”经过半小时,甲船在B处追上了乙船.求: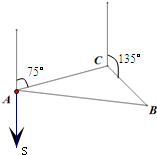
| 14 |
| 0.5 |
| AB |
| sinC |
| BC |
| sinA |
| 14 |
| sin120° |
| 6 |
| sinA |
| 3 |
| 7 |
3
| ||
| 14 |
| 14 |
| 0.5 |


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
 如图,某海域中有甲、乙两艘测量船分别停留在相距(
如图,某海域中有甲、乙两艘测量船分别停留在相距(| 6 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:044
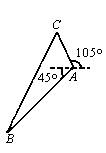
甲船在A处遇险,在甲船正西南10n mile处的乙船收到甲船的报警后,测得甲船是沿着方位角105°的方向,以每小时9n mile的速度向某岛靠近,如果乙船要在40min内追上甲船,则乙船应以多少速度,以何方向航行?(如图所示)
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
查看答案和解析>>
科目:高中数学 来源:2013年江苏省高考数学模拟试卷(五)(解析版) 题型:解答题
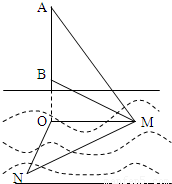 如图,某海域中有甲、乙两艘测量船分别停留在相距(
如图,某海域中有甲、乙两艘测量船分别停留在相距(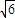
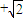 )海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON=2
)海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON=2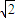 海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.
海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com