
 A组:直角坐标系xoy中,已知中心在原点,离心率为
A组:直角坐标系xoy中,已知中心在原点,离心率为| 1 |
| 2 |
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
 A组:
A组:| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
| 1 |
| 2 |
| x2 |
| 16 |
| y2 |
| 12 |
| 1 |
| 2 |
| |2k1+y0-k1x0| | ||||
|
| 2 |
| k | 2 1 |
| y | 2 0 |
| k | 2 2 |
| y | 2 0 |
|
| y02-2 |
| (2-x0)2-2 |
| 1 |
| 2 |
| x02 |
| 16 |
| y02 |
| 12 |
| 18 |
| 5 |
| 18 |
| 5 |
| ||
| 5 |
| 18 |
| 5 |
| ||
| 5 |
| 18 |
| 5 |
| ||
| 5 |
| c |
| a |
| 1 |
| a2 |
| c2 |
| a2b2 |
| ||
| 2 |
| e2 |
| a2 |
| 3 |
| 4b2 |
| a2-1 |
| a4 |
| 3 |
| 4 |
| x2 |
| 2 |
|
m+
| ||
| m2+2 |
| ||||
| m2+2 |
| ||||
| m2+2 |
2m
| ||
| m2+2 |
2m
| ||
| m2+2 |
| ||
| 2 |
| 2 |
| 1 |
| m |
| ||
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
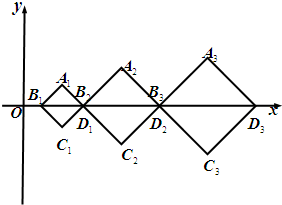 (2009•上海)如图,在直角坐标系xOy中,有一组对角线长为an的正方形AnBnCnDn(n=1,2,…),其对角线BnDn依次放置在x轴上(相邻顶点重合).设{an}是首项为a,公差为d(d>0)的等差数列,点B1的坐标为(d,0).
(2009•上海)如图,在直角坐标系xOy中,有一组对角线长为an的正方形AnBnCnDn(n=1,2,…),其对角线BnDn依次放置在x轴上(相邻顶点重合).设{an}是首项为a,公差为d(d>0)的等差数列,点B1的坐标为(d,0).查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省张掖中学高二(上)期中数学试卷(解析版) 题型:解答题
 的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心.
的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心. 的直线l1,l2.当直线l1,l2都与圆C相切时,求P的坐标.
的直线l1,l2.当直线l1,l2都与圆C相切时,求P的坐标. 的左、右焦点分别为F1(-c,0),F2(c,0).已知点(1,e)和
的左、右焦点分别为F1(-c,0),F2(c,0).已知点(1,e)和 都在椭圆上,其中e为椭圆离心率.
都在椭圆上,其中e为椭圆离心率. ,求直线AF1的斜率.
,求直线AF1的斜率.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省张掖中学高二(上)期中数学试卷(解析版) 题型:解答题
 的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心.
的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心. 的直线l1,l2.当直线l1,l2都与圆C相切时,求P的坐标.
的直线l1,l2.当直线l1,l2都与圆C相切时,求P的坐标. 的左、右焦点分别为F1(-c,0),F2(c,0).已知点(1,e)和
的左、右焦点分别为F1(-c,0),F2(c,0).已知点(1,e)和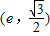 都在椭圆上,其中e为椭圆离心率.
都在椭圆上,其中e为椭圆离心率. ,求直线AF1的斜率.
,求直线AF1的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com