
(1)当x∈[2k-1,2k+1](k∈Z)时,求f(x)的表达式;?
(2)若f(x)的最大值为![]() ,解关于x的不等式f(x)>
,解关于x的不等式f(x)>![]() .
.
解析:(1)当x∈[-1,0)时,f(x)=f(-x)=loga[2-(-x)]=loga(2+x).?
当x∈[2k-1,2k)(k∈Z)时,x-2k∈[-1,0),f(x)=f(x-2k)=loga[2+(x-2k)];?
当x∈[2k,2k+1](k∈Z)时,x-2k∈[0,1],f(x)=f(x-2k)=loga[2-(x-2k)].
故当x∈[2k-1,2k+1](k∈Z)时,f(x)的表达式为?
f(x)=?
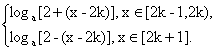
(2)∵f(x)是以2为周期的周期函数,且为偶函数,
∴f(x)的最大值就是当x∈[0,1]时,f(x)的最大值.?
∵a>1,∴f(x)=loga(2-x)在[0,1]上是减函数.?
∴f(x)max=f(0)=loga2=![]() .?
.?
∴a=4.?
当x∈[-1,1]时,由f(x)>![]() 得
得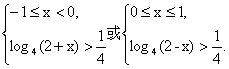 ?
?
得![]() -2<x<2-
-2<x<2-![]() .?
.?
∵f(x)是以2为周期的周期函数,?
∴f(x)> ![]() 的解集为{x|2k+
的解集为{x|2k+![]() -2<x<2k+2-
-2<x<2k+2-![]() ,k∈Z}.
,k∈Z}.


科目:高中数学 来源: 题型:
A.![]() B.
B.![]() C.
C.![]() D.1-
D.1-![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
A.2 B.2或1 C.3 D.2或3
查看答案和解析>>
科目:高中数学 来源: 题型:
A.2 B.2或1 C.3 D.2或3
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)是定义域为R的奇函数,-2是它的一个零点,在(0,2)内无零点,且在(2,+∞)上是增函数,则该函数有________个零点,这几个零点的和等于________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)是定义域为R的奇函数,-2是它的一个零点,在(0,2)内无零点,且在(2,+∞)上是增函数,则该函数有________个零点,这几个零点的和等于________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com