
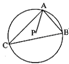
 如图,点P为△ABC的外心,且|
如图,点P为△ABC的外心,且|| AC |
| AB |
| AP |
| AC |
| AB |
科目:高中数学 来源:湖北黄冈骆驼坳中学2008届高三第一轮复习综合检测题(数列、三角、向量) 题型:013
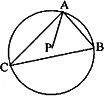
如图,点P为△ABC的外心,且![]() ,则
,则![]() 等于
等于
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:高中数学 来源:天利38套《2008全国各省市高考模拟试题汇编 精华大字版》、数学理 题型:013
如图,点P为△ABC的外心,且|![]() |=4,|
|=4,|![]() |=2,则
|=2,则![]() ·(
·(![]() -
-![]() )等于
)等于
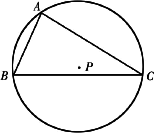
A.2
B.4
C.6
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com