
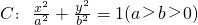 的长半轴是短半轴的
的长半轴是短半轴的 倍,直线
倍,直线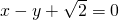 经过
经过 ,求△AOB面积的最大值.
,求△AOB面积的最大值.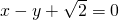 与x轴的交点为
与x轴的交点为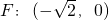 ,
,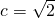
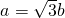 ,c2=a2-b2=2
,c2=a2-b2=2 ,b=1
,b=1 . (5分)
. (5分)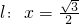 ,
,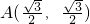 、
、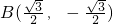
 、
、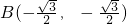
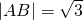 (6分)
(6分)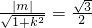 ,得
,得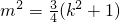 .
.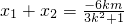 ,
,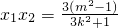 .
.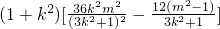 =
=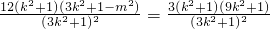 =
=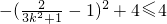 . (12分)
. (12分)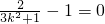 ,即
,即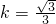 时等号成立.
时等号成立.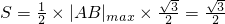 .(14分)
.(14分)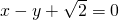 经过椭圆C的一个焦点,可求c.利用长半轴是短半轴的
经过椭圆C的一个焦点,可求c.利用长半轴是短半轴的 倍,可求椭圆C的方程;
倍,可求椭圆C的方程;

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| ab |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010年上海市高二下学期期中考试数学 题型:解答题
1. 我国计划发射火星探测器,该探测器的运行轨道是以火星(其半径 百公里)的中心
百公里)的中心 为一个焦点的椭圆. 如图,已知探测器的近火星点(轨道上离火星表面最近的点)
为一个焦点的椭圆. 如图,已知探测器的近火星点(轨道上离火星表面最近的点) 到火星表面的距离为
到火星表面的距离为 百公里,远火星点(轨道上离火星表面最远的点)
百公里,远火星点(轨道上离火星表面最远的点)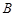 到火星表面的距离为800百公里. 假定探测器由近火星点
到火星表面的距离为800百公里. 假定探测器由近火星点 第一次逆时针运行到与轨道中心
第一次逆时针运行到与轨道中心 的距离为
的距离为 百公里时进行变轨,其中
百公里时进行变轨,其中 、
、 分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).
分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).

查看答案和解析>>
科目:高中数学 来源:2009-2010学年广东省深圳市五校高三联考数学试卷(理科)(解析版) 题型:解答题
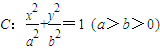 的长半轴是短半轴的
的长半轴是短半轴的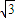 倍,直线
倍,直线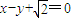 经过
经过 ,求△AOB面积的最大值.
,求△AOB面积的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com