若数列{a
n},{b
n}中,a
1=a,b
1=b,
| | an=-2an-1+4bn-1 | | bn=-5an-1+7bn-1 |
| |
,(n∈N,n≥2).请按照要求完成下列各题,并将答案填在答题纸的指定位置上.
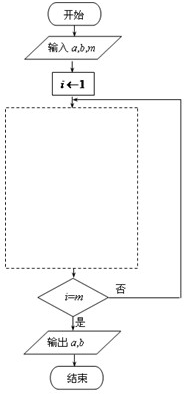
(1)可考虑利用算法来求a
m,b
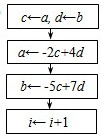
m的值,其中m为给定的数据(m≥2,m∈N).右图算法中,虚线框中所缺的流程,可以为下面A、B、C、D中的
ACD
ACD
(请填出全部答案)
A、
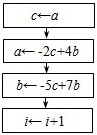
B、
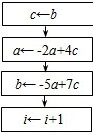
C、
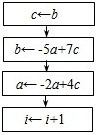
D、
(2)我们可证明当a≠b,5a≠4b时,{a
n-b
n}及{5a
n-4b
n}均为等比数列,请按答纸题要求,完成一个问题证明,并填空.
证明:{a
n-b
n}是等比数列,过程如下:a
n-b
n=(-2a
n-1+4b
n-1)+(5a
n-1-7b
n-1)=3a
n-1-3b
n-1=3(a
n-1-b
n-1)
所以{a
n-b
n}是以a
1-b
1=a-b≠0为首项,以
3
3
为公比的等比数列;
同理{5a
n-4b
n}是以5a
1-4b
1=5a-4b≠0为首项,以
2
2
为公比的等比数列
(3)若将a
n,b
n写成列向量形式,则存在矩阵A,使
=A=A(A)=A2=…=An-1,请回答下面问题:
①写出矩阵A=
; ②若矩阵B
n=A+A
2+A
3+…+A
n,矩阵C
n=PB
nQ,其中矩阵C
n只有一个元素,且该元素为B
n中所有元素的和,请写出满足要求的一组P,Q:
; ③矩阵C
n中的唯一元素是
2n+2-4
2n+2-4
.
计算过程如下:

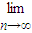 (1+a+a2+…+an-1)=9,则实数a等于 .
(1+a+a2+…+an-1)=9,则实数a等于 .  中考解读考点精练系列答案
中考解读考点精练系列答案 若数列{an},{bn}中,a1=a,b1=b,
若数列{an},{bn}中,a1=a,b1=b, B、
B、
 D、
D、