
 且两场比赛之间相互独立,用ξ表示甲选手比赛结束后的奖金总额.
且两场比赛之间相互独立,用ξ表示甲选手比赛结束后的奖金总额.科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 12 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:2012届吉林省延吉市高二下学期期末考试数学(理) 题型:解答题
在某电视台举办的《上海世博会知识有奖问答比赛》中,甲、乙、丙三人同时回答一道问题,已知甲回答对这道题的概率是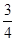 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是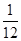 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是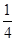 ,且三人答对这道题的概率互不影响.
,且三人答对这道题的概率互不影响.
(1)求乙、丙两人各自回答对这道题的概率;
(2)求答对该题的人数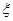 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源:2010年四川省攀枝花市高考数学三模试卷(理科)(解析版) 题型:解答题
 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是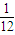 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是 ,且三人答对这道题的概率互不影响.
,且三人答对这道题的概率互不影响.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com