
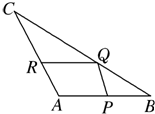
 如图,△ABC是一块边长AB=3m,AC=5m,BC=7m的剩余角料.现要从中裁剪出一块面积最大的平行四边形用料APQR,要求顶点P,Q,R分别在边AB,BC,CA上.问点Q在BC边上的什么位置时,剪裁符合要求?并求这个最大值.
如图,△ABC是一块边长AB=3m,AC=5m,BC=7m的剩余角料.现要从中裁剪出一块面积最大的平行四边形用料APQR,要求顶点P,Q,R分别在边AB,BC,CA上.问点Q在BC边上的什么位置时,剪裁符合要求?并求这个最大值. | 11 |
| 14 |
| 13 |
| 14 |
5
| ||
| 14 |
3
| ||
| 14 |
| xsinB |
| sin120° |
| (7-x)sinC |
| sin120° |
| x(7-x)sinBsinC |
| sin120° |
15
| ||
| 98 |
| 7 |
| 2 |
15
| ||
| 8 |
15
| ||
| 8 |


科目:高中数学 来源: 题型:
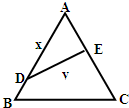 如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省南通市如皋中学高三(上)第一次月考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com