
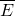 为“射中7环或8环或9环或10环”,由(1)可知“射中7环”“射中8环”等是彼此互斥事件.
为“射中7环或8环或9环或10环”,由(1)可知“射中7环”“射中8环”等是彼此互斥事件.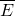 )=0.21+0.23+0.25+0.28=0.97,
)=0.21+0.23+0.25+0.28=0.97,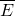 )=1-0.97=0.03.
)=1-0.97=0.03.

 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)射中10环或7环的概率;
(2)不够7环的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
某射手在一次射击训练中,射中10环、9环、8环、7环的概率分别为0.21、0.23、0.25、0.28,计算这个射手在一次射击中:
(1)射中10或7环的概率;
(2)不够7环的概率.
查看答案和解析>>
科目:高中数学 来源:2013届江苏省高二2月测试数学试卷(解析版) 题型:解答题
某射手在一次射击训练中,射中10环、9环、8环、7环的概率分别为
0.21,0.23,0.25,0.28,计算该射手在一次射击中:
(1) 射中10环或9环的概率;(2)少于7环的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com