
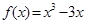 ,过点P
,过点P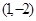 的直线
的直线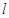 与曲线
与曲线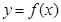 相切,求
相切,求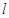 的方程;
的方程; ,当
,当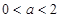 时,
时,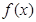 在1,4上的最小值为
在1,4上的最小值为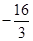 ,求
,求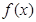 在该区间上的最大值.
在该区间上的最大值.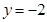 或
或  (2) 最大值为
(2) 最大值为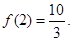
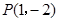 ,但是并没有说明该点是不是切点,所以得设出切点坐标,根据导数的几何意义可知,曲线切线的斜率就是在切点横坐标处的导数,然后利用点斜式求得切线方程;代入点
,但是并没有说明该点是不是切点,所以得设出切点坐标,根据导数的几何意义可知,曲线切线的斜率就是在切点横坐标处的导数,然后利用点斜式求得切线方程;代入点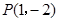 可求出切点,从而得切线方程.
可求出切点,从而得切线方程.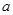 的范围可判断出函数在所给区间
的范围可判断出函数在所给区间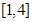 上的单调性,从而得出在该区间上的最小值(含
上的单调性,从而得出在该区间上的最小值(含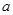 ),令其等于
),令其等于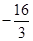 可得
可得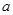 ,从而求出在该区间的最大值.
,从而求出在该区间的最大值.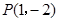 ,但是并没有说明该点是不是切点,所以设切点为
,但是并没有说明该点是不是切点,所以设切点为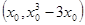 ,
,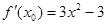 ,
,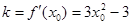 ,
,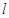 的方程
的方程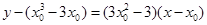 .
.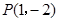 ,所以
,所以 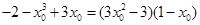 ,
,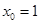 或
或 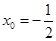
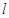 的方程为
的方程为 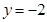 或
或 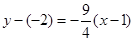 ,
,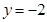 或
或  .
.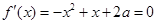 得
得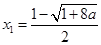 ,
,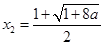 ,
,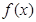 在
在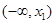 上递减,在
上递减,在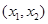 上递增,在
上递增,在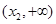 上递减.
上递减.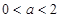 时,有
时,有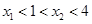 ,所以
,所以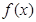 在
在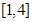 上的最大值为
上的最大值为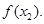
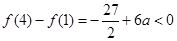 ,即
,即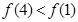 .
.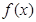 在
在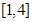 上的最小值为
上的最小值为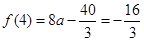 ,得
,得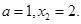
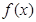 在
在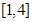 上的最大值为
上的最大值为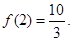


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com