
【题目】设各项均为正数的数列{an}的前n项和为Sn , 满足an+1= ![]() ,n∈N* , 且a2 , a5 , a14构成等比数列.
,n∈N* , 且a2 , a5 , a14构成等比数列.
(1)求数列{an}的通项公式;
(2)若对一切正整数n都有 ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() ,求实数a的最小值.
,求实数a的最小值.
【答案】
(1)解:当n≥2时,可得:4Sn= ![]() ﹣4n﹣1,4Sn﹣1=
﹣4n﹣1,4Sn﹣1= ![]() ﹣4(n﹣1)﹣1,
﹣4(n﹣1)﹣1,
相减可得:4an=4Sn﹣4Sn﹣1= ![]() ﹣
﹣ ![]() ﹣4,化为:
﹣4,化为: ![]() =
= ![]() ,∵an>0,∴an+1=an+2,即an+1﹣an=2,
,∵an>0,∴an+1=an+2,即an+1﹣an=2,
∴当n≥2时,数列{an}是公差为2的等差数列.∵a2,a5,a14构成等比数列.∴ ![]() =a2a14,
=a2a14,
∴ ![]() =a2(a2+12×2),解得a2=3.
=a2(a2+12×2),解得a2=3.
又n=1时,3=a2= ![]() ,解得a1=1.∴a2﹣a1=3﹣1=2.
,解得a1=1.∴a2﹣a1=3﹣1=2.
∴数列{an}是公差为2的等差数列,∴an=1+2(n﹣1)=2n﹣1
(2)解: ![]() =
= ![]() =
= ![]() .
.
∴ ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() +…+
+…+ ![]() =
= ![]() .
.
由 ![]() ≤
≤ ![]() ,a≥
,a≥ ![]() .
.
∴实数a的最小值为 ![]()
【解析】(1)由Sn和an 的关系可求出数列{an}是公差为2的等差数列,再由已知可得a2,a5,a14构成等比数列,利用等比数列的定义可求出a2=3。根据已知递推公式可得a1=1,a2=3所以可求出公差d=2进而得到数列{an}是公差为2的等差数列。(2)根据(1)整理由裂项相消法求和得到代数式,由放缩法可得该式小于![]() ,进而得到a的最小值。
,进而得到a的最小值。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点P(2,0),曲线C的参数方程为 ![]() (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系. (Ⅰ)求曲线C的普通方程和极坐标方程;
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系. (Ⅰ)求曲线C的普通方程和极坐标方程;
(Ⅱ)过点P且倾斜角为 ![]() 的直线l交曲线C于A,B两点,求|AB|.
的直线l交曲线C于A,B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
B餐厅分数频数分布表 | |
分数区间 | 频数 |
[0,10) | 2 |
[10,20) | 3 |
[20,30) | 5 |
[30,40) | 15 |
[40,50) | 40 |
[50,60] | 35 |

(Ⅰ)在抽样的100人中,求对A餐厅评分低于30的人数;
(Ⅱ)从对B餐厅评分在[0,20)范围内的人中随机选出2人,求2人中恰有1人评分在[0,10)范围内的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() +c(e=2.71828…是自然对数的底数,c∈R).
+c(e=2.71828…是自然对数的底数,c∈R).
(Ⅰ)求f(x)的单调区间、最大值;
(Ⅱ)讨论关于x的方程|lnx|=f(x)根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的最小正周期为4π,则( )
的最小正周期为4π,则( )
A.函数f(x)的图象关于原点对称
B.函数f(x)的图象关于直线 ![]() 对称
对称
C.函数f(x)图象上的所有点向右平移 ![]() 个单位长度后,所得的图象关于原点对称
个单位长度后,所得的图象关于原点对称
D.函数f(x)在区间(0,π)上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A、B是海面上两个固定观测站,现位于B点南偏东45°且相距 ![]() 海里的D处有一艘轮船发出求救信号.此时在A处观测到D位于其北偏东30°处,位于A北偏西30°且与A相距
海里的D处有一艘轮船发出求救信号.此时在A处观测到D位于其北偏东30°处,位于A北偏西30°且与A相距 ![]() 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非零平面向量 ![]() ,
, ![]() ,则“|
,则“| ![]() |=|
|=| ![]() |+|
|+| ![]() |”是“存在非零实数λ,使
|”是“存在非零实数λ,使 ![]() =λ
=λ ![]() ”的( )
”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,平面PAC⊥平面ABC,PA⊥AC,AB⊥BC.设D,E分别为PA,AC中点.
(Ⅰ)求证:DE∥平面PBC;
(Ⅱ)求证:BC⊥平面PAB;
(Ⅲ)试问在线段AB上是否存在点F,使得过三点 D,E,F的平面内的任一条直线都与平面PBC平行?若存在,指出点F的位置并证明;若不存在,请说明理由.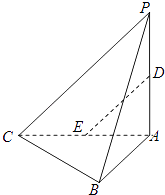
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com