
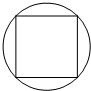
 某次游园的一项活动中,设置了一个中奖方案:在如图所示的游戏盘内转动一个小球,如果小球静止时停在正方形区域内则中奖.这个方案中奖率是多少?请说明理由.
某次游园的一项活动中,设置了一个中奖方案:在如图所示的游戏盘内转动一个小球,如果小球静止时停在正方形区域内则中奖.这个方案中奖率是多少?请说明理由. 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:2012-2013学年广东省珠海市高一(下)期末数学试卷B(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com